- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
gcd of more than 2 numbers
11-24-2006 06:07 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
chris
CL(A)Dly bending G-Force with LabVIEW
famous last words: "oh my god, it is full of stars!"
11-24-2006 07:04 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
11-24-2006 07:17 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Gerd,
well, ok...:-) there has been a coding challenge "prime factors" some time ago, i'll take a look at the code i can found there.
chris
CL(A)Dly bending G-Force with LabVIEW
famous last words: "oh my god, it is full of stars!"
11-24-2006 08:21 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
hi there
i found something useful at http://zone.ni.com/devzone/cda/epd/p/id/1005
based on Ben Buhrows code i could find a solution for my needs (I32, value < 1.000.000). see attachment (sorry, no valid zipper round here...).
chris
CL(A)Dly bending G-Force with LabVIEW
famous last words: "oh my god, it is full of stars!"
04-11-2019 09:42 AM - edited 04-11-2019 09:43 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
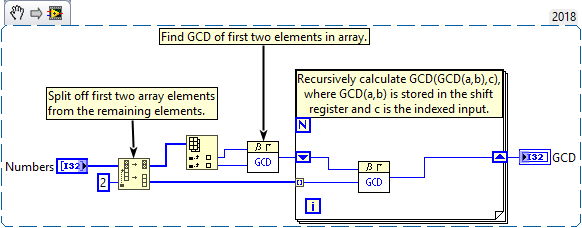
For anyone coming across this now, this is a much more performant and easier to understand solution:
It recursively uses the shipping GCD VI instead of using the prime factor method. (I suspect that the GCD VI didn't exist back in 2006 when this post was originally made.) VI is attached.
04-15-2019 02:26 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@croohcifer wrote:
For anyone coming across this now, this is a much more performant and easier to understand solution:
(Be careful with the wording, this has nothing to do with recursion. I am also not sure what "much more performant" means. Do you have relevant benchmarks?)
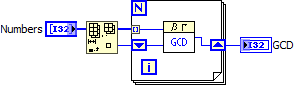
In any case. Your version still seems overly complicated. You only need exactly one instance of GCD.
Here is equivalent, but arguably simpler code. 😄
04-16-2019 08:54 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks for calling out my sloppy use of "recursion" and for providing the simplified code! Yes, I did benchmark it per Darren's brainless LabVIEW benchmarking best practices to be multiple orders of magnitude faster than the original solution. Here's the snippet for those looking:
04-16-2019 09:04 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
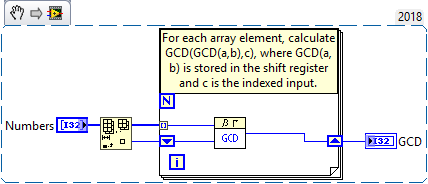
We could make a recursive version, if that is a requirent or goal of some sort (homework?).
We could make a VI that calculates the GCD of a number and an array. If the array >1 element, strip a number and call the VI.
Altough that would be pointless, overcomplicated and wasteful, it will be recursion. ![]() .
.
04-16-2019 09:20 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@croohcifer wrote:
Yes, I did benchmark it per Darren's brainless LabVIEW benchmarking best practices to be multiple orders of magnitude faster than the original solution.
Most likely things could be improved even further by taking advantage of the fact that we are dealing with an array. For example if we would sort the array in a certain way first and then use code tailored to that fact. I have not tried.
04-16-2019 09:28 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I don't doubt that. In my case, I was just trying to find the GCD of the sample rates of data sets captured across several (5-10) different instruments running at various rates. I used this post as a starting point, spent about 15 minutes improving it, saw massive gains, and moved on. For much larger data sets where performance is critical, I'm sure more mathematically capable folks than me could come up with something stellar 🙂