ni.com is currently undergoing scheduled maintenance.
Some services may be unavailable at this time. Please contact us for help or try again later.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Extract inner XY coordinates
Solved!08-16-2017 04:57 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
I need to calculate the area "inside" the collection of given XY coordinates, basically the inner part of the XY graph.
In know how to calculate area for XY coordinates but I can't figure out how to extract the "inner" ones from this collection.
I hope I was clear... ...
All inputs are welcome!
Regards
Alain
Solved! Go to Solution.
08-16-2017 07:21 AM - edited 08-16-2017 07:22 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
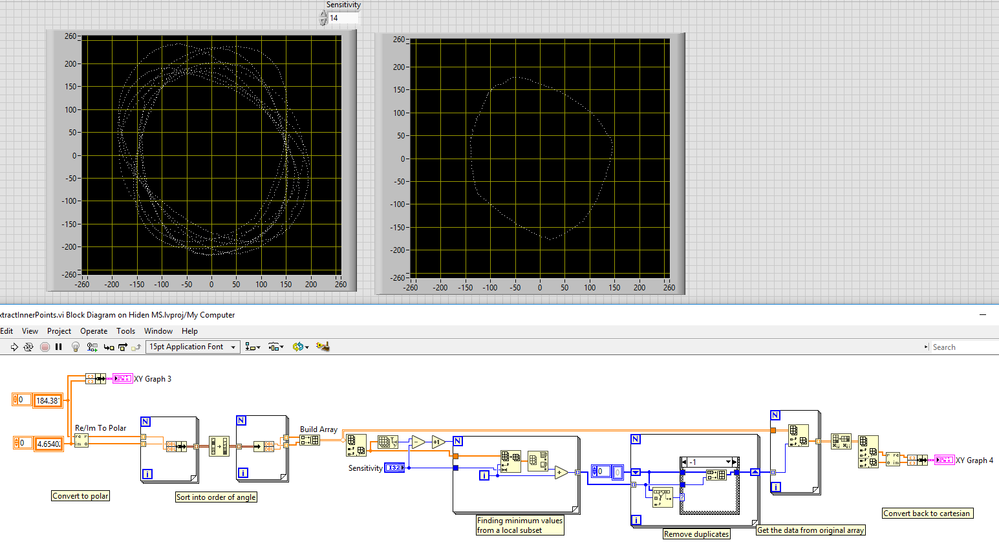
I have attempted this with your data.
Adjusting the Sensitivity gives fewer or more points, for your data a sensitivity of 14 gave the optimum result. It would scale with how many "loops" your data has, I suggest using double the number of loops.
File attached.
I noticed you used LV2012, so have not utilised the sort 2D array function from LV2017 (or the OpenG one, for ease of sharing)
There may be easier ways which I have missed, and this may be able to be optimised (I've assumed the dataset is small), but this one gives a fairly good set of "inner" XY coordinates. You mentioned you could do the rest.
Let me know if it works for you.
08-16-2017 07:38 AM - edited 08-16-2017 07:40 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
08-16-2017 08:45 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
Thanks for quick and accurate answer.
I tried this method on several datasets, all works fine!
Best regards!
08-16-2017 12:30 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
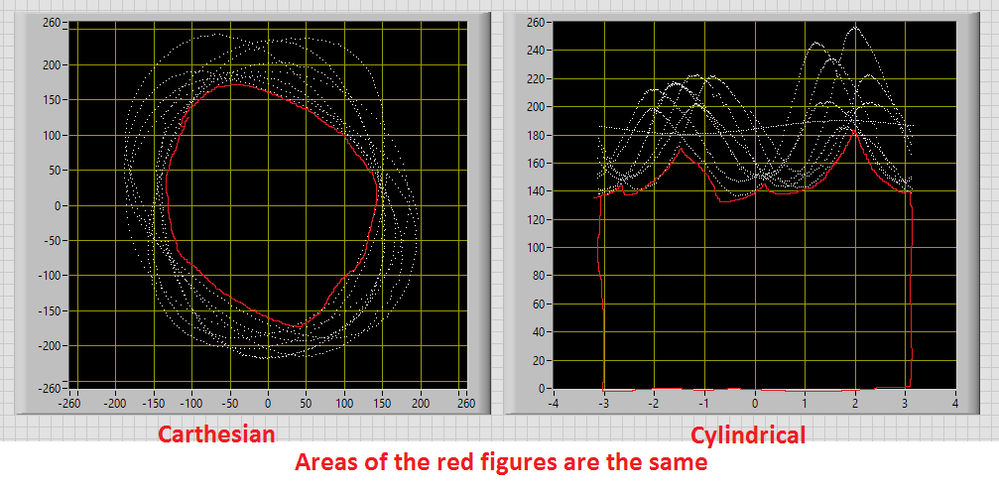
I'm just interested, why would this be easier:
"try converting carthesian coordinates to cylindrical. Then calculate the area under the points clouds, which might be easier:"
08-17-2017 01:32 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@alexderjuengere wrote:
I'm just interested, why would this be easier:
"try converting carthesian coordinates to cylindrical. Then calculate the area under the points clouds, which might be easier:"
As in IanSh solution - you need to find minimum "edge" of the points cloud and then integrate (sum) area under this edge. I can't exactly find the direct way to calculate this area in original (carthesian) representation, but I can think about a few ways to do it in polar* coordinates.
*I've used conversion from carthesian to polar with Z values = 0. This is the same as converting Re/Im To Polar - I just didn't yet read enough altenbachs posts to immediately think about 2D planes with complex numbers ;D
08-17-2017 03:08 AM - edited 08-17-2017 03:11 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
PiDi wrote:
... ... .. I can't exactly find the direct way to calculate this area in original (carthesian) representation, but I can think about a few ways to do it in polar* coordinates
[url=https://en.wikipedia.org/wiki/Shoelace_formula] CLICK [/url]
08-17-2017 03:23 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Neat, I hadn't thought about looking up that part as you had said you have a solution. Of course LabVIEW has a function already for this.
You can use Polygon Area.vi to calculate the area. I just looked inside, it actually uses this same shoelace formula ![]()
In fact, you may find other useful functions in Mathematics>Geometry>Computational Geometry. Never been inside that palette before.
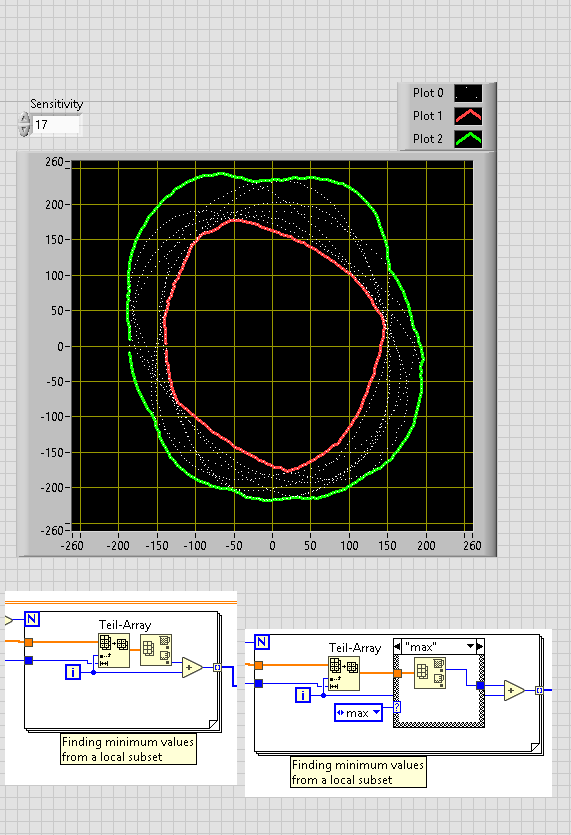
It will be quite important (I expect) to make sure the sensitivity is set correctly, as a single outlying point may throw your answer off a bit.
08-17-2017 05:01 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@Alain_S wrote:
@PiDi wrote:
... ... .. I can't exactly find the direct way to calculate this area in original (carthesian) representation, but I can think about a few ways to do it in polar* coordinates
[url=https://en.wikipedia.org/wiki/Shoelace_formula] CLICK [/url]
Ok, wrong wording, I wanted to say that finding the internal points is harder, no the area calculation itself 😉 Thanks for the link though!
08-17-2017 05:51 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@PiDi wrote:
*I've used conversion from carthesian to polar with Z values = 0. This is the same as converting Re/Im To Polar - I just didn't yet read enough altenbachs posts to immediately think about 2D planes with complex numbers ;D
Indeed, I like that your implementation with "3d coordinate conversion.vi" can be easily extend to a 3d space
Moreover, I personally like about IanSh .vi, that it is very easy to find the edge points of the point cloud
Kudos to all of you