- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
help with downhill optimization
Solved!01-28-2011 08:13 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi all,
I am trying to solve this one equation with one unknown using optimization. It's a non-linear equation and I was searching around for something that works like excel's solver. The downhill optimization seems close to what I want to do, but it is not optimizing. Would anyone mind looking at this code and try to determine what I'm doing wrong?
FYI, I've checked the answer by putting 0.02 as the X in my function and it is giving the right value. The function is set up to be like: Calc(X) - Actual = 0. The "=0" portion should be implied (maybe this is what is wrong?)
Thanks,
Matt
Solved! Go to Solution.
01-28-2011 08:55 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
The problem seemed to be the initial value of your function and the type of your function. If you try to plot it, you will notice the discontinuity around 21.049 as shown below:
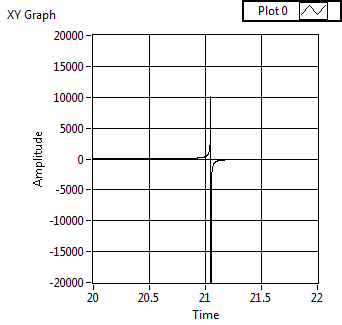
If you start from the left (like 21) then the minimization function will only be able to converge. If you start on the right (like 22), then you will find the X = 21.049 as minimum.
Here is the code for it:
Hope this helps
01-28-2011 09:14 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I just noticed that... If you are trying to get the Func - Measured, then you are trying to detect zero crossing of it instead of minimum. In this case, then you have to make the f(x) present the minimum when crossing zero. You can use the minimization function but you have to change f(x) to be abs(f(x)). Then, finding the minimum means detecting where the function crosses zero.
If this also doesn't help, maybe it would be good to have your original problem posed and, if possible, which function you were trying to use in Excel.
01-28-2011 09:40 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
ahh thank you! I will try the absolute value when I get in the office on Monday. In the meantime, I coded a simple Newton Rahpson method to work with my function that seems to do the job as well.
Thanks again!
Matt
01-28-2011 09:42 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
oh also I do not expect solutions above 21%... in fact, all answers should be greater than zero but less than 5%. You must be correct that I need to do the absolute value and give it a better first approximation.
Thanks,
Matt
01-29-2011 09:47 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thank you! The absolute value did the trick!
Thanks again!
Matt

