Algorithm that can calculate the shortest path between 0-360 degrees for an AC servo motor.

[tst]

I think I understand what constructionworker is asking for.

Is this correct:

1. Angle can only be between 0-360 and indicates the current direction the motor is pointing at.
2. Position can be any number and indicates the total accumulation of the motions performed by the motor. For instance, start at position 10 (and angle 10) and move two revolutions CCW and you're now at position -710 and angle 10. Because this is a servo motor, I don't think you would get the actual position tracked by the motor, but you can track it on your own.
3. You want to enter an angle between 0-360, calculate the closest position to the current position which matches that angle and then tell the motor to move X degrees CW or CCW to get to that position. For example, if you are at position 750 (angle 30) and ask for angle 350, the command to the motor should be to move -40 degrees and end up at position 710.

Correct?

[constructionworker]

---

@tst wrote:

I think I understand what constructionworker is asking for.

Is this correct:

1. Angle can only be between 0-360 and indicates the current direction the motor is pointing at.
2. Position can be any number and indicates the total accumulation of the motions performed by the motor. For instance, start at position 10 (and angle 10) and move two revolutions CCW and you're now at position -710 and angle 10. Because this is a servo motor, I don't think you would get the actual position tracked by the motor, but you can track it on your own.
3. You want to enter an angle between 0-360, calculate the closest position to the current position which matches that angle and then tell the motor to move X degrees CW or CCW to get to that position. For example, if you are at position 750 (angle 30) and ask for angle 350, the command to the motor should be to move -40 degrees and end up at position 710.

Correct?

---

Yes, that's exactly it. oh, I think the situation has cleared up a bit 🙂

[constructionworker]

---

@Bob_Schor wrote:

You are confounding "position" and what I will call "pseudo-velocity".  Position, as you have defined it with your circular disk label 360, 10, 20, ... 340, 350 (going clockwise) are the only possible "positions" (well, there's an ambiguity, as Position 0 = Position 360 -- another way to define "Position" is "Angle clockwise from straight up mod 360", so one complete clockwise revolution = 360° = 0° (because 360 mod 360 = 0).  Let's define "Rotate CW from X by Y" as (X + Y) mod 360, and "Rotate CCW from X by Y" as (X - Y) mod 360.  So if you start at 10 and rotate CCW by 50, you get to (10 - 50) mod 360 = 320.  You can (by definition) never get to a negative position because Position is always 0 .. 360.

So take any two positions, A and B.  Start at A and make a single Rotation (of some amount) to get to B.  If you are going Clockwise, you need to move by Ycw such that B = A + Ycw, or Ycw = (B - A) mod 360, and if CCW, B = A - Yccw, or Yccw = (A - B) mod 360.  Choose the direction that has the smaller value (they'll both be non-negative, of course).

Example -- you are at 15, and want to go to 50.  Ycw = (50 - 15) mod 360 = 35.  Yccw = (15 - 50) mod 360 = 325.  Go CW (because 35 < 325).  [Notice that Ycw + Yccw will always be 0 mod 360].

Another example -- you are at 15, and want to go to 350.  Ycw = (350 - 15) mod 360 = 335.  Yccw = (15 - 350) mod 360 = 25.  Go CCW (because 25 < 335).

Bob Schor

---

I have to say it again
- I will enter  values between 0-360 from numerical control. However, negative degrees can be sent to the motor depending on the degree the motor stands.

-Yes, 0=360 degrees. In other words, if we start the motor from 0 and move forward, when I finally reach 360 degrees, the motor  comes back to the same place.

Example -- you are at 15, and want to go to 50.  Ycw = (50 - 15) mod 360 = 35.  Yccw = (15 - 50) mod 360 = 325.  Go CW (because 35 < 325).  [Notice that Ycw + Yccw will always be 0 mod 360].

---

- I think there is another misunderstanding.The values that the user will enter from the "numeric control" should actually be between 0-359.99. This is because 0==360.

-if I apply the example of Ycw = (50 - 15) mod 360 = 35.
This means:
I'm CW 10 degrees and I want to go 50 degrees. If I write 35 degrees, the motor goes to 35 degrees. Not 50 degrees.

If I apply the example here. Yccw = (15 - 50) mod 360 = 325
This means:

-The motor is now at 15 degrees CW.

-and I'm sending positive 325 degrees to the motor.

-The motor will have used a long way in the CW direction. And it will reach 325 degrees.

[tst]

---

@constructionworker wrote:

---

@tst wrote:

I think I understand what constructionworker is asking for.

Is this correct:

1. Angle can only be between 0-360 and indicates the current direction the motor is pointing at.
2. Position can be any number and indicates the total accumulation of the motions performed by the motor. For instance, start at position 10 (and angle 10) and move two revolutions CCW and you're now at position -710 and angle 10. Because this is a servo motor, I don't think you would get the actual position tracked by the motor, but you can track it on your own.
3. You want to enter an angle between 0-360, calculate the closest position to the current position which matches that angle and then tell the motor to move X degrees CW or CCW to get to that position. For example, if you are at position 750 (angle 30) and ask for angle 350, the command to the motor should be to move -40 degrees and end up at position 710.

Correct?

---

Yes, that's exactly it. oh, I think the situation has cleared up a bit 🙂

---

Then I believe all you need to is desired angle - current angle mod 360. If this is < 180, just move by that amount CW. Otherwise, you need to subtract it from 360 and move by that amount CCW. I think this covers all of your cases, but I haven't run the numbers.

To get the current angle, you just need to calculate the current position mod 360.

[wiebe@CARYA]

---

@constructionworker wrote:

---

@tst wrote:

I think I understand what constructionworker is asking for.

Is this correct:

1. Angle can only be between 0-360 and indicates the current direction the motor is pointing at.
2. Position can be any number and indicates the total accumulation of the motions performed by the motor. For instance, start at position 10 (and angle 10) and move two revolutions CCW and you're now at position -710 and angle 10. Because this is a servo motor, I don't think you would get the actual position tracked by the motor, but you can track it on your own.
3. You want to enter an angle between 0-360, calculate the closest position to the current position which matches that angle and then tell the motor to move X degrees CW or CCW to get to that position. For example, if you are at position 750 (angle 30) and ask for angle 350, the command to the motor should be to move -40 degrees and end up at position 710.

Correct?

---

Yes, that's exactly it. oh, I think the situation has cleared up a bit 🙂

---

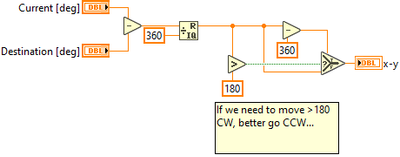
Doesn't this do that?

Note Current and Destination switched from the previous example that look like this.

When 750 and 350 are entered, -40 is the result...

[constructionworker]

---

@tst wrote:

---

🙂

---

Then I believe all you need to is desired angle - current angle mod 360. If this is < 180, just move by that amount CW. Otherwise, you need to subtract it from 360 and move by that amount CCW. I think this covers all of your cases, but I haven't run the numbers.

To get the current angle, you just need to calculate the current position mod 360.

---

If I didn't misinterpret what you said, you're talking about something like the following, right?
If so, this is not exactly what is wanted.

---

wiebe@CARYA wrote:

---

Doesn't this do that?

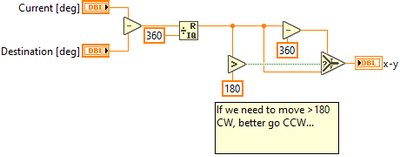
Note Current and Destination switched from the previous example that look like this.

When 750 and 350 are entered, -40 is the result...

---

It doesn't do exactly what you want here.

I should also mention that the user must enter degrees in the range of 0-360 in "numerical control". Depending on the degree to which the motor is currently stopped, only negative or positive degrees can be sent to the motor.

[tst]

---

@constructionworker wrote:

---

---

wiebe@CARYA wrote:

---

Doesn't this do that?

Note Current and Destination switched from the previous example that look like this.

When 750 and 350 are entered, -40 is the result...

---

It doesn't do exactly what you want here.

---

Why not? What do you expect to get and what do you actually get?

---

@constructionworker wrote:

---

@tst wrote:

---

🙂

---

Then I believe all you need to is desired angle - current angle mod 360. If this is < 180, just move by that amount CW. Otherwise, you need to subtract it from 360 and move by that amount CCW. I think this covers all of your cases, but I haven't run the numbers.

To get the current angle, you just need to calculate the current position mod 360.

---

If I didn't misinterpret what you said, you're talking about something like the following, right?
If so, this is not exactly what is wanted.

---

No, I suggested what Wiebe showed.

I'm not sure what you're doing here, but you again seem to mix up what I called position and angle. I would suggest that you make it very clear when you are using each of them and make sure you don't mix them. Once you calculated the number of degrees to move, you need to add that to the current position to get the new position.

[constructionworker]

---

@tst wrote:

---

@constructionworker wrote:

---

---

wiebe@CARYA wrote:

---

Doesn't this do that?

Note Current and Destination switched from the previous example that look like this.

When 750 and 350 are entered, -40 is the result...

---

It doesn't do exactly what you want here.

---

Why not? What do you expect to get and what do you actually get?

---

@constructionworker wrote:

---

@tst wrote:

---

🙂

---

Then I believe all you need to is desired angle - current angle mod 360. If this is < 180, just move by that amount CW. Otherwise, you need to subtract it from 360 and move by that amount CCW. I think this covers all of your cases, but I haven't run the numbers.

To get the current angle, you just need to calculate the current position mod 360.

---

If I didn't misinterpret what you said, you're talking about something like the following, right?
If so, this is not exactly what is wanted.

---

No, I suggested what Wiebe showed.

I'm not sure what you're doing here, but you again seem to mix up what I called position and angle. I would suggest that you make it very clear when you are using each of them and make sure you don't mix them. Once you calculated the number of degrees to move, you need to add that to the current position to get the new position.

---

I tried what wiebe@CARYA suggested. But the problem is that if I give commands to start at 0 degrees and rotate in CCW direction it calculates positions incorrectly.
For example, let's say I type 350 degrees into the "Target" control.
-Because the engine has to go 350 degrees from the nearest road
-The algorithm should return the number of degrees -10.
-and I need to send this returned value to the engine.
-The engine will come to the 350 position. This is exactly what is wanted.

But as seen in the photo below,

first problem:

if ''Current degree'' is 25, when ''Destination Degree'' is written as 50, ''x+Y'' should be 50 NOT -25.

second problem:

I mean for the example in the picture above. Here - shouldn't be a negative number because rotations in the CW direction require + degrees, for CCW turns - degrees.

Third problem: I'm talking about the algorithm in the picture above.
What if the motor is moved to the CCW in small steps of no more than 180 degrees and the motor has to turn to the CCW because the next location is the nearest road?
- Let me give  an example. -10..-60..-120..-180...-250...-350..-359... -365...-420..
It should continue to turn in this way as long as the commands given do not require a reverse turn and as long as the commands are given in the CCW turn direction.

This algorithm is not available in the example above and is currently the most challenging problem.

[Bob_Schor]

I give up.  To me, the problem seems very simple and conceptual -- one has a rotary positioner with a rotary "position indicator", with the following properties:

1. The Positioner can rotate either CW or CCW for an arbitrary distance (including an arbitrary number of full revolutions).
2. Position is specified in Degrees, in the interval [0, 360).  This notation means that 0 is included in the range, but 360 is not (when it gets to what would be 360, it auto-resets to 0, so Position is expressed as a non-negative number mod 360).
3. To move from Position A to Position B, you want to make the shortest movement that takes you from A to B.  This will result in a CW or CCW rotation between 0 and 180 (whereas going in the other direction will be between 360 and 180).

My algorithm does this.  I think the confusion lies in sloppy definitions of terms.  I'll check back in a week and see if this has been resolved.

Bob Schor

[altenbach]

---

@Bob_Schor wrote:

My algorithm does this.  I think the confusion lies in sloppy definitions of terms.  I'll check back in a week and see if this has been resolved.

---

I am out too. I'd give it at least a month. (... and like the position indicator, this thread will be going in circles for another few pages of posts. :D.)