- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
exponential fit - revisited.
Solved!07-12-2012 12:22 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi - I keep thinking I should be getting a lot better fit results on my decaying exponential for both exponential models and all calculation methods possible in the attached VI (modified from LabVIEW example, so all subVIs should be available within LabVIEW).
I don't necessarily want to have to provide initial parameter bounds.
Any thoughts?
Sincerely,
Don
Solved! Go to Solution.
07-12-2012 12:46 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
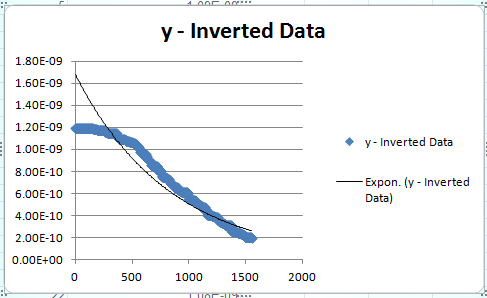
Here is what I obtain using Excel - which is closer to what I would expect.
07-13-2012 04:03 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
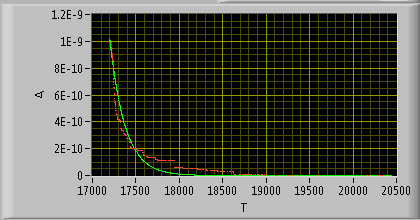
Hi DonRoth, can you post an screenshot of what are our results in LabVIEW?
07-13-2012 04:18 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Your curve is not a decaying exponential, but something entirely different. What are you trying to get out of all this?
Your data covers an extremely small Y range, thus you need to adjust the termination condition accordingly.
Also the paramters seem to differ bu huge orders of magnitude, making the fit somewhat ill conditioned.
07-13-2012 04:37 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Things come out looking very different if you graph the input (white) and curve fit (red) on an XY plot. Maybe the X-axis values aren't evenly spaced?
07-13-2012 05:39 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Wart - You nailed it. I forgot I had unevenly-spaced X data.
The exponential + offset works if I supply a very large number for estimate of a (amplitude in the model a*exp(bt) + c).
Christian - I actually agree with you that exponential model will not provide the best fit. However, on this project, there is literature in which this model is used for some experimental data and depending on the value of b, some conclusions seem to be able to be drawn.
Sincerely,
Don