Wrong math in "LM get new coefficients.vi" of Levenberg Marquardt fitting

[Herbert]

Hi folks,

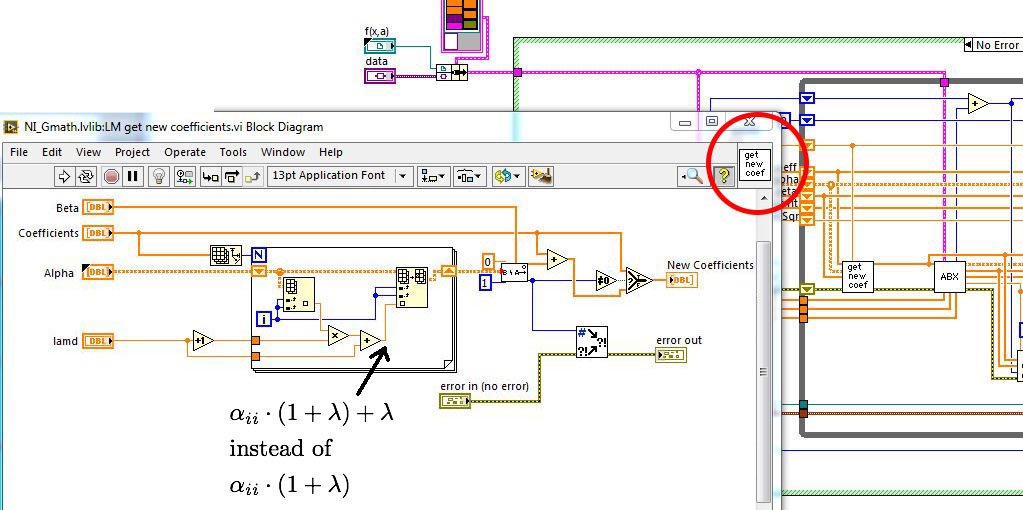
fortunately, I wrote my own LM-Fit algorithm a long time ago, an algorithm that I optimized for speed. Lately however, I used the LM-nonlinear fit off the shelf - and - wondered about its bad convergence. I then checked the source code and found the coding below:

No wonder. My derivatives were numerically of order 10^-7 meaning that the alpha's were something like 10^-14. Due to the wrong formula, the algorithm thus stepped into the (1, 1, 1, 1, ...) direction. It ignored the calculated gradient completely, as the value of lambda is 10 on start up (due to the 15 digits numerical precision of Dbl).

I am posting my findings although I will not be astonished, if this obvious error will not be corrected for years.

My negative attitude comes from a similar posting of mine, about two or three years ago, where I reported and documented the exponential fit to be mathematically week and unreliable. After a first positive response, nothing happened anymore, the same code is still in LV2014.   I know, most people seem to be happy and mostly it works - so what?

Herbert

[Herbert]

Hi folks,

I apologize - I posted the same bug three years ago, but not so clear as now.

Because I had forgotten about and stumbled once more upon this error, I felt bad to not to issue a warning to general users (it is not that I want to ponder on this issue).

Truth is: The bug is still in, reported three years ago. NI seems to be happy with wrong algorithms, as long as most people don't realize and are happy.

Herbert

[altenbach]

It is not wrong, just different as explained by Jim long ago. (more robust if there are correlations)

(I use my own version that can select between the two options. :D)

[Herbert]

Sorry

[Herbert]

I am no longer talking about the lambda values as then but about the formula "alpha_ii*(1+lambda) + lambda".

First: Can you tell me, how walking into the opposite direction can create a more robust algorithm, i.e. if for example the gradient says to go to (-1, -1, -1, ...) while you go to (1, 1, 1, ..)? This is the fact that I am opposing and this is done in that formula: In two dimensions, the most robust way, according to you and NI in these cases, is to always start into the 45° direction, discarding any information from your data. I question this method to be either optimal nor robust. It's success depends on numerical jitter due to limited precision.

Second: How can a formula, being wrong with respect to unities (alpha_ii/sigma^2 has physical meaning - maybe numerically unknown till the end of the fitting, while lambda is a dimensionless fudge factor) result in a more robust algorithm? Lambda determines, as Jim and others explain, the transition between steepest descent and Newton and depends only no the convergence history of the algorithm and not on experimental precision. How can such an algorithmic property be added to a property with physical meaning -  I don't understand and oppose.

Herbert

[Intaris]

I (don't understand) and (oppose)

-or-

I don't (understand and oppose)

[altenbach]

---

@Intaris wrote:

I (don't understand) and (oppose)

---

(old, thread, I know)

I actually don't understand the question or argument. The diagonal elements of alpha are guaranteed to be positive (code uses absolute weights) and have nothing to do with walking in a certain direction.