Why does high-pass filtering distort data?

[koukileo]

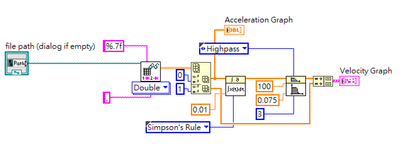
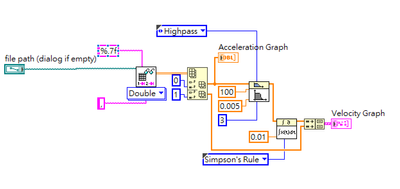
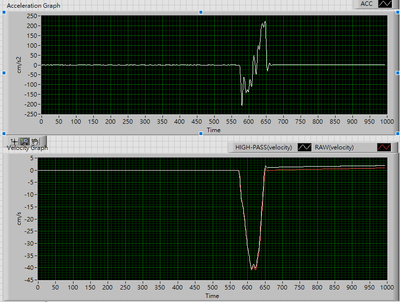
I am using an MCU to interrupt and read accelerometer data at a rate of 100Hz, and I want to calculate displacement. However, when I move the accelerometer, there inevitably appears to be an offset (zero calibration was performed at initialization) Many articles mention that high-pass filtering the velocity can make the calculation of displacement more accurate. However, as you can see from the diagram, once I apply a high-pass filter to the velocity signal, the signal becomes strange with bumps appearing. Is there any way to solve this? PS. I have attached the data (without high-pass filtering, and the actual displacement is around 19.7cm). X represents acceleration, Y represents velocity after the first integration, and Z represents displacement after the second integration.

[JÞB]

Well, your cutoff frequency is 100 hz and the Nyquist frequency is 50hz.   That is going to provide poor results. Try a cutoff around 20Hz 

[koukileo]

100Hz is the sampling frequency, and 0.075 is the cutoff frequency.

 

[Kevin_Price]

I haven't done much with high-pass filtering so am not equipped to explain the tail end of the curve that looks similar to exponential decay.  I'm more familiar with low-pass filtering (though I'm not exactly an expert there either).

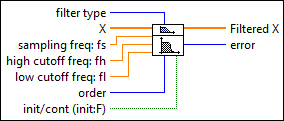
In any event, I would think you should be doing your high-pass filter *before* the integration step.  The purpose of the high-pass filter is to reject DC offset and near-DC drift so you don't integrate them into a velocity ramp or drift.  So you need to filter first, integrate second.

-Kevin P

[rpursley8]

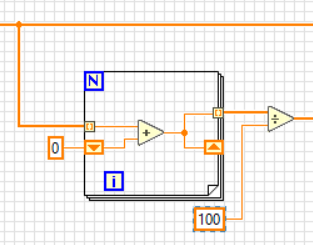
I think the problem is the integration function.  You have no starting values defined. If I were you I would just generate a running sum of your data to do the integration shown below.  That way, you don't have to worry about the initial conditions.  With the high-pass filter you just might set the cutoff to 0.005 Hz or lower just to isolate the DC value.  Kevin_P is correct in that the high-pass filter should be first.

[koukileo]

Even if I put the filter at the very beginning (acceleration), there is still no difference. 0.005Hz is too low, causing the offset to not be corrected.😞

[koukileo]

I'm curious how those who make IMUs can integrate for such a long time without drifting. I think there must be high-pass ? Because the accelerometer must have a DC offset.

https://www.youtube.com/watch?v=6ijArKE8vKU

[Jjohnn]

The decay after the pulse looks very similar to the effect of high pass filters I have seen on pulsed waveforms.

Applying a high pass filter to a pulsing waveform I saw an overshoot and droop on the tops of the pulses.  You can demonstrate this by high pass filtering a square wave signal.

I am not sure if my interpretation is correct, but I think of a high pass filter as trying to drive the mean to zero.

So in general, high pass filters can cause droops, and low pass filters slow down the edges and broaden pulses.

You might consider just calculating the offsets before and after the pulse and subtracting the trend from the pulse itself.

[Bob_Schor]

All filtering "distorts" the data!  What you really want to do is to "distort" away the "noise", and be left with "the signal".

I'm a little confused about what you are doing and what/how you are measuring.  Are you using a 1-axis or a tri-axial accelerometer?  Can you describe the motion of the accelerometer?  Is it constrained to move in a straight line, and does this align with an accelerometer axis?

If you measure acceleration and want to plot velocity, you need to integrate the acceleration.  Integration acts as a low-pass filter -- I'm not sure why you are high-pass filtering the acceleration signal (thereby increasing the well-known "noise-to-signal ratio").  But then, I'm not an engineer ...

Bob Schor