PID control oscillation

[Blokk]

Hi,

Just for the reference (so we must use parallel mode of course):

two Keithley 2400 connected in parallel

regards

[nathand]

---

Blokk wrote:

Just for the reference (so we must use parallel mode of course):

two Keithley 2400 connected in parallel

---

Were you able to reduce the oscillation by doing this?

[Blokk]

I will only travel to the location by plane in March. I monitor the device and program LabView via remote desktop... I will need to be there physically to do the new wiring for the two Keithleys (i want to do it myself).

For the reference, I will post here in March with the results with the two sourcemeters.

Regards,

[Blokk]

Hello,

I have tested my PID control with using two Keithley 2400 sourcemeter. I have created an algorithm, what first only uses the Keithley#1 (+-1 A range) to PID control the water temperature ("coarse mode"). When the system reaches equilibrium with the problematic oscillation (about half an hour period time), the algorithm fixes the output of the Keithley#1 and turns on the Keithley#2 output used in a lower output range. So actually I send the output value of the PID minus the fixed current of the Keithley#1 to the Keithley#2 sourcemeter.

The above VI works well, the two Keithley sourcemeters can properly control the Peltier heat-pump, nice to see the Kirchoff law in work 🙂  (the two sourcemeters are connected in parallel, so their outputs' algebraic sum drives the Peltier pump array).

BUT. The above upgrade did not stop the discovered process value oscillation, I have the same result like with only using one sourcemeter in 1A range. I also tried 100 mA and 10 mA range in the second Keithley, no improvement 😞

What I want to try now, that I do a different PID control tuning method. I tuned this control loop with closed loop Ziegler-Nichols method, but since this is a circulated water loop with quite a large volume = heat capacity, I guess there is some time lag in the system, so maybe it is better now to try to tune my system with the open-loop Cohen-Coon method...? What do you think?

Thanks for any advice!

Regards,

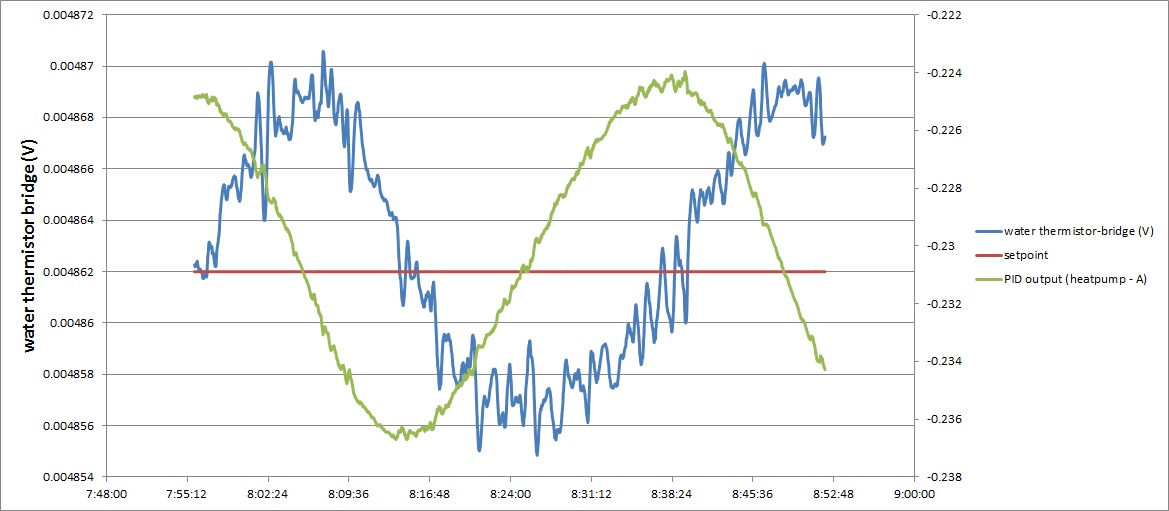
ps.: i have attached the tipical oscillation what I have, the PV with the output.

[johnsold]

It is interesting that over the duration of the data you posted the oscillation period seems to be increasing.  That implies that some characteristic of the system is changing.

If the system is variable, the controller may need to be adaptive to compensate.

Can you try running it for a time so the that oscillation is present and as "stable" as it gets, then switch the controls so that the Keithleys are producing a constant output with a value near the mean value from the previous cycle or two.  Of course the temperature will probably rise or fall under those conditions, but hopefully the rate will be slow. I am curious whether the temperature change will be linear under those conditions.

Another consideration: Can you use feedforward control to correct for part of this behavior?  If the amplitude and freqeuncy are well known, this might help.

Lynn

[Blokk]

"It is interesting that over the duration of the data you posted the oscillation period seems to be increasing.  That implies that some characteristic of the system is changing."

Well, it is only because I was "lazy" to wait enough, if I wait until the system gets into stable oscillation, the period time and the amplitude of the PV and PID output are quite constant...

Can you try running it for a time so the that oscillation is present and as "stable" as it gets, then switch the controls so that the Keithleys are producing a constant output with a value near the mean value from the previous cycle or two.  Of course the temperature will probably rise or fall under those conditions, but hopefully the rate will be slow. I am curious whether the temperature change will be linear under those conditions.

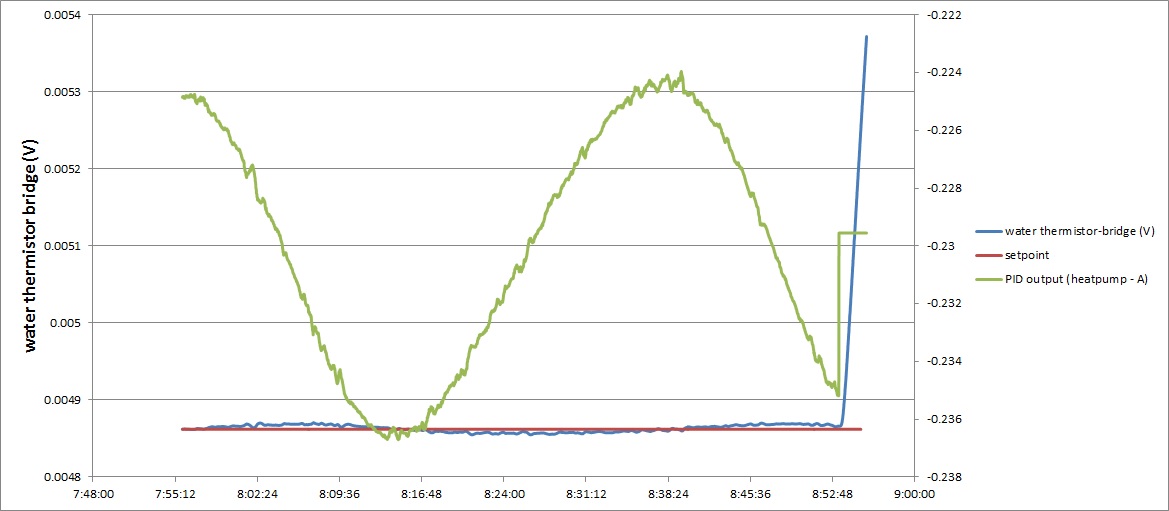
I will do this, and I will post here the results as the above jpg file. So I will switch the system (after some time when everything is stable) to manual mode, and set the output to an average calculated from 1 or 2 previuos periods what were recorded.  Actually what I know already: if I apply a constant driving current in manual mode, the response looks quite linear I think, but I will try this anyway again so I can save the data and show it...

Another consideration: Can you use feedforward control to correct for part of this behavior?  If the amplitude and freqeuncy are well known, this might help.

Can you give some hints here? I know there is this "PID Lead-Lag.VI" but my knowledge in control theory is quite limited.

Just some guessing how to use this VI with the PID.VI, please correct me if I misunderstand something:

1., I have to put this lead-lag VI "between" the ProcessValue and the PID input.

2., Since the water has a high heat capacity, it responds with a lag to the driving current.

        Tuning parameters:   Gain = 1 I guess since I do not want to change the proportional gain, lag = some value, LEad = this should be zero i guess...

   So I need to specify the phase lag. What is phase lag? I guess, this is the waiting time, until the PV curve reacts for the PID output change. If I look at the jpg graph with PV and output plotted, I would estimate this to be roughly 10 minutes. Am I right?

Thanks very much for help! (and I feel very soon I must start to learn control theory fundamentals 🙂 )

Best Regards,

[Blokk]

Dear Johnsold,

Here comes the result of the test you asked for:

the quite stable oscillation (i did not disturbe the system overnight):

And the effect of switching the output current to a fix value (average of the last 1 hour):

I have also attached the raw data in an Excel file, in case you need some more close look.

Recently I am trying to use the PID advanced autotuning VI, in Step Closed Loop technique, I hope it will refine my existing PID parameters to better ones...

But anyhow, I am still interested in any other advices and ideas to try, like the mentioned feed-forwarding. I tried that one actually only once so far, with 9 minutes lag time, but the system went to instable state.

Thanks again for help,

Best Regards,

[nathand]

I just want to confirm: in the second graph, the output is held constant and not shown on the graph? The PID output shown is meaningless, since the PID is disconnected? When I rescale that graph to match the upper one, I see the same oscillation. If the output is being held constant and it still oscillates, then it's being generated by something outside the PID loop, and the PID is trying to compensate for it.

[Blokk]

hello, the second graph is the same as the first, but contains some additional minutes: where I fix the PID output, and I send this to the current generator.

You can see here, the process value, the temperature starts to run up with...

the green(ish) line is the PID output on both graphs

[Blokk]

tomorrow I will try to start this fixed output at the very same time when the recent output has the same value as the average, hopefully the PV change rate will be smaller, and we can see if there is oscillation without the PID control or not....