- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Inflection point from second derivative
02-14-2010 11:20 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi all,
I'm trying to find the inflection point of a discrete set (10-20 points) of measured data.
I thought I would use the second derivative test. Is this the best way?
The first step would be to calculate the second derivative function for my data (I may need to interpolate?).
Please refer to the attached VI. The simple function y = 3x^2 should have an inflection (strictly speaking it's a turning point) at x = 0. Therefore y''(0) = 0.
The problem is that the VI does not return the second derivative equal to zero. It is even worse for 10 datapoints.
I'm wondering if anyone can help.
Thanks,
Battler.
02-15-2010 04:01 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello battler,
You should be careful with your math: if y=3x^2, then first derivative is y'=6x and second derivative is y''=6, i.e. a constant and not y''(0)=0.
What exactly do you mean by "inflection point" ? See this in wikipedia: http://en.wikipedia.org/wiki/Inflection_point
What do you want to find ?
Does your discrete set of data contain experimentally obtained values that have only finite accuracy (and have therefore some error) ? If so, then simple derivation could be quite problematic.
Unfortunately I cannot open your .vi since I have LV 8.5.2
regards,
Bojan
02-15-2010 06:00 AM - edited 02-15-2010 06:04 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
If your aim is to find points where the gradient changes sign (Usually a minimum or maximum) I have used a for loop with the point by point differentiation to find the gradient (I am fairly sure this is the first derivitive). Using this in conjunction with a threshold where i expect minima or maxima to be (Only checks the gradient above or below a threshold).
i.e dy/dx of x^2 at x=o => 2x0 = 0.
dy/dx of x^2 at x=-1 => 2x-1 = -1,
dy/dx of x^2 at x=1 => 2x1 = 1,
If gradient changes sign and is above / below said threshold that is your point you are looking for.
The second derivitive is rate of change of gradient. i.e is the gradient getting steeper than my curent gradient. (Acceleration in comparison to speed for example)
Craig
02-15-2010 06:55 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator

Besides which, my opinion is that Express VIs
(Sorry no Labview "brag list" so far)
02-15-2010 08:26 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
If your function is quadratic (ie to the second power) it does not have an inflection point.
An inflection point is when the function changes from positive first derivative to negative or visa versa.
This only occurs in functions with powers 3 or greater
02-15-2010 03:38 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks for your replies guys.
It was a typo: I meant x^3.
All of you should read this:
Second derivative test
From Wikipedia, the free encyclopedia
- If
then
has a local maximum at
.
- If
then
has a local minimum at
.
- If
, the second derivative test says nothing about the point
, a possible inflection point.
In the last case, although the function may have a local maximum or minimum at x, because the function is sufficiently "flat" (i.e. ) the extremum is rendered undetected by the second derivative. In this case one has to examine the third derivative. The point at which
is an inflection point if concavity changes on either side of it. For example, (0,0) is an inflection point on
because
, and
and
.
02-15-2010 03:50 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Finding (possible) inflection point for discrete x, y test data:
The way my algorithm works:
1. Convert X-values to equal spacings (required for discrete differentiation).
2. Apply spline interpolation to discrete x (at equal spacing), y.
3. Differentiate twice using discrete Derivative x(t) with dt as equal spacing determined in Step 1.
4. Index f''(x) array and check for change in sign (i.e. zero crossing). If True then between the current and previously indexed values there is an inflection point.
5. Fit a linear curve between the two points. Using the linear equation find the zero crossing (i.e. y=0). This is close to where the inflection point occurs.
I will try to post the VI once completed.
Any suggestions, please make them.
02-15-2010 07:33 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Dear battler,
You still did not tell us what is the origin of your datapoints. If they have a significant amount of noise added, then a more robust algorithm is needed. The location of the inflection point as given by your algorithm will depend entirely on few datapoints around it and if you slightly change a value of any of them, the location of the inflection point my shift significantly. In other words: if you have noisy datapoints, you can have a significant error bar on the location of the inflection point.
regards,
Bojan
02-16-2010 03:36 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Coq Rouge
I hear you which is why i tune this type of vi from case to case to get the point I am looking for. I dont usually use at all for finding definitive points more for array subsets / meas triggers etc. have used it successfully in the past in a robust manner, but only if i can predict what i am trying to measure. i.e a pulse above a threshold etc. Out of interest what methods do you use for finding these type of points? (Always open to a better way of doing things) 🙂
Craig
02-16-2010 04:13 AM - edited 02-16-2010 04:16 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
craigc wrote:Coq Rouge
I hear you which is why i tune this type of vi from case to case to get the point I am looking for. I dont usually use at all for finding definitive points more for array subsets / meas triggers etc. have used it successfully in the past in a robust manner, but only if i can predict what i am trying to measure. i.e a pulse above a threshold etc. Out of interest what methods do you use for finding these type of points? (Always open to a better way of doing things) 🙂
Craig
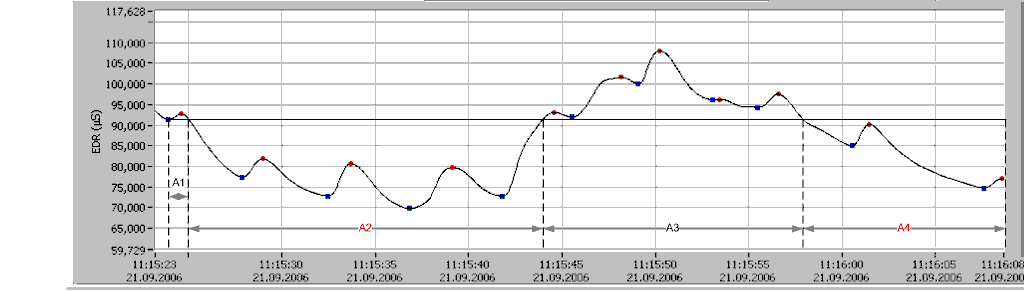
I have used Labview peak detection functions. Not the Express VI version of course. With some extra application specific fine tuning this will work well in most cases. The picture is a random example from my computer. The picture is somewhat edited but the blue and red dots are from Labview, and not edited

Besides which, my opinion is that Express VIs
(Sorry no Labview "brag list" so far)