Impact force measured using an accelerometer mounted on the bullet - urgent please

[StathPol]

No worries Bill 🙂 .. Yes, I have learnt a lot from these guys here and I am grateful to them.

[johnsold]

Since the presence or absence of hte steel rod appears to make very little difference in the resonant behavior, I started thinking about other options.

My thought now is that the 3.5 kHz oscillation is always there (after being excited by the initial impact). The high frequency noise may be due to the propagation of the crack in the concrete.

Can you post some of the raw impact data? Something like the data shown in your first post in this tread. Run your VI until that data is shown on an array or graph indicator. Stop it. Right click on the indicator and select Make Current Value Default. Save and then post that VI. Note that it must be a graph, not a chart. If you cannot do that with a VI, a text file containing the data will work. With actual data we can try things in an attempt to understand what is going on.

Lynn

[StathPol]

I went back in the lab night-time to test a concrete sample in order to post the data.

The array data were imported in an excel file.

The first two columns indicate the acceleration - time readings for a test including the steel rod. The columns D and E indicate the test without the steel rod. In both cases, concrete sample has failed in flexure.

[StathPol]

I went back to look at the frequencies of previous tests.  Two tests are the data that I posted in the previous post.

As aforementioned, the first two columns indicate the acceleration of the bullet including the steel rod and the other two columns indicate the acceleration of the bullet without the steel rod. In both cases, the concrete has cracked.

When the bullet was tapped using an impact hammer, in both cases (with steel rod and without) the frequency of 3.5 kHz is the same.

I have attached the results in the excel file.

[Ben]

Can you please test what is the resonant freq of the detector by itself?

Ben

[StathPol]

Hi Ben,

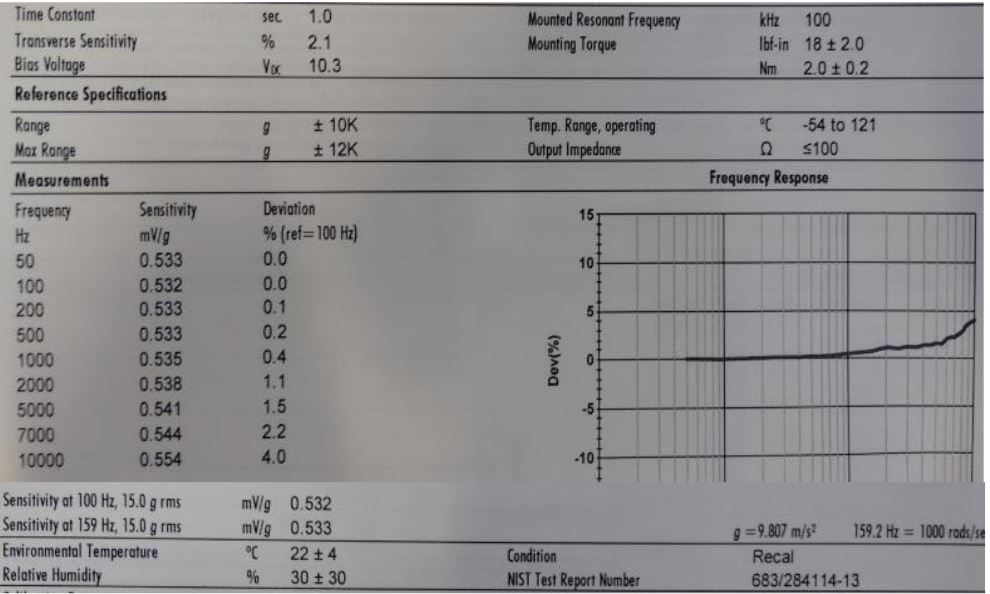
Thanks. If the detector stands for the accelerometer,then the reasonant frequency is 100 kHz.

[StathPol]

Would a rigid solid piece of high strength steel bullet solve the problem? No steel rod, no nothing. Just an accelerometer mounted in the middle of the bullet.

[Henrik_Volkers]

---

@StathPol wrote:

Would a rigid solid piece of high strength steel bullet solve the problem? No steel rod, no nothing. Just an accelerometer mounted in the middle of the bullet.

---

No, just other resonance frequencies...

What usually helps, is to shift  annoying resonances to regions where you can filter them 🙂    .. so a ball isn't that bad...

Exactly what do you want to measure/test?   

One reason why you often have test standards (with exactly defined masses/shapes) is that even if you have such problems, they are the same for the same test. That doesn't mean that the test is still meaningful to answer your question, but it's reproduceable 😄

And for the modal impact hammer test of your steel body (half ball) : hit the body at the same point where the impact force to the concrete applies.  You migth find other modals ...

[StathPol]

To measure the acceleration of the bullet and then convert the signal to impact force F=mxa.

The good thing is that the test is repeatable, however the issue is to find the correct impact force graph without any external influences.

And for the modal impact hammer test of your steel body (half ball) : hit the body at the same point where the impact force to the concrete applies.  You migth find other modals ...

Near the accelerometer >?

[Henrik_Volkers]

---

@StathPol wrote:

To measure the acceleration of the bullet and then convert the signal to impact force F=mxa.

The good thing is that the test is repeatable, however the issue is to find the correct impact force graph without any external influences.

And for the modal impact hammer test of your steel body (half ball) : hit the body at the same point where the impact force to the concrete applies.  You migth find other modals ...

Near the accelerometer >?

---

No, at the point where the body hits the concrete. Maybe that was already one of your tests ...

and F=m*a is only part of the truth if you have an elastic body and only one accelerometer at the top 😉  

I don't know how big the differences are.. a FEM of your impact body with a F(t)  at the impact point  might put some light on it. (and then there is Hertz, also in your impact body not only in the concrete)