Image Moment - Optimizing Code for Speed

[johnsold]

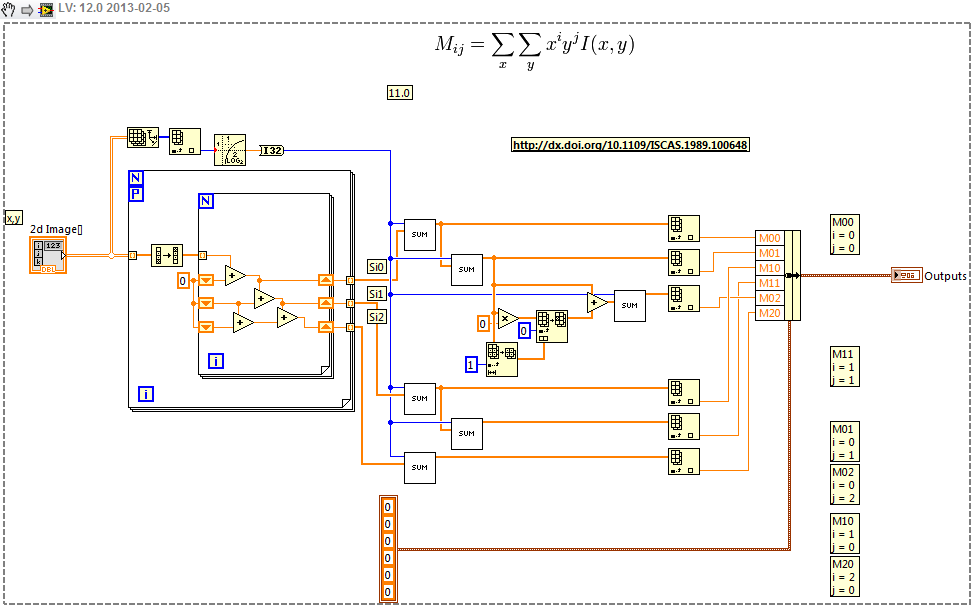
After looking at some simple calculations, I wonder if the algorithm cited uses summations starting with x=1 and y=1? It does not explicitly state the limits. The way you have implemented the calculation in LV (which uses zero-based indexing), the first row and column are always multiplied by zero, effectively removing them from the moment calculation.  Consider M11 for a 3x3 array:

M11 = 0*0*A[0,0] + 0*1*A[0,1] + 0*2*A[0,2]

        +1*0*A[1,0] + 1*1*A[1,1] + 1*2*A[1,2]

        +2*0*A[2,0] + 2*1*A[2,1] + 2*2*A[2,2]

       =  1*1*A[1,1] + 1*2*A[1,2]

         +2*1*A[2,1] + 2*2*A[2,2]

If you decide to use summations starting at 1, the technique Paul suggested (preparing the x and y arrays in advance) becomes even more advantageous.

Lynn

[johnsold]

I spent some time on this. (OK, more time than I should have spent).

I coded several of the things which have been proposed along with a few others. I also put together a test VI (test moment speed.vi) to evaluate the execution time of the various approaches.  The one called Image Moment.2.vi is the original code, modifed slightly for the test VI.  The modifcations  were primarily the output cluster so that the results of each subVI can be compared.  The test VI creates a square 2D data array of the size specified by the user.  I did not take great care about data copies so larger arrays (<4096x4096) may cause out of memory errors. The data in the array can be random in the range of 0..4095 or fixed with all elements = 4095.  For the algorithms which use precalculated arrays for x, x^2, y, and y^2, the size is  automatically reduced to the size of the array. (Note: This does not work correctly for data arrays larger than 2048x2048.) The start index can be selected to be 0 or 1.

Image Moment.3.f.vi, Image Moment.3.g.vi, and Image Moment.4.f.vi use the precalculated x and y arrays and are the only subVIs which can start the x and y values at 1.  Running with Start Index = 0 allows verification that they generate the same results as the others (to 6 significant figures).

Image Moment.4.f.vi uses integer calculations with all integers set to U64, which is big enough to represent the largest value of the moments.  The results differ from the DBL calculation for M11 after the 6th digit. I did not explore the difference.

Timing: I used the flat sequence structure and Tick Count to determine the time of execution. All subVI front panels were closed. The fastest were 3.f, 2.f, and 2.e with very little difference among the three.  All of these calculate x and y outside the for loops. The integer calculations (4.f) were only slightly faster than the original code. The fastest versions calculate the moments of a 2048x2048 array in about 80 ms compared to 120 ms for the original.

I got a bunch of warnings when I saved this for an earlier version, so if it does not open or execute, let me know.

Lynn

[SectorEffector]

@flakpl

You state your images are 0-4096- this is a 12 bit number, you are converting this to a double (64bit numbers), I assumed  your IMAQ image was either a I 16 or U16, is this correct?

[SectorEffector]

@johnsold

You really put time and effort in it! You are making me feel bad! Thank you very much.

I hope NI will put this calculation in there Vision IMAQ package, a DLL doing this would be 10 times faster I think.

[GregSands]

I'd also recommend using SGLs if you can for a 2x speedup and memory reduction - I've converted most of my own image processing code to SGL, and have no problems with accuracy for what I use it for (includes deconvolution).

A quick Google search led to Fast algorithm for the calculation of image moments in a linear processor array which computes vertical and horizontal components separately using only additions, no multiplications.  Took just a few minutes to code up.  It is ~3x faster than the fastest of the above implementations (for 2048x2048), and if the intial loop is parallelized, even on my 2-core machine, it is ~10x faster.  It would probably be well suited to a GPU or FPGA implementation.  The algorithm uses a Start Index of 1.

Here's my timing results with a parallel loop:

The algorithm:

and the Sum routine is:

[SectorEffector]

Thank you GregS

Did you buy the algorithm to answer here in the forum? If so I would like that everyone who reads this thread gives you kudos!

[SectorEffector]

GregS

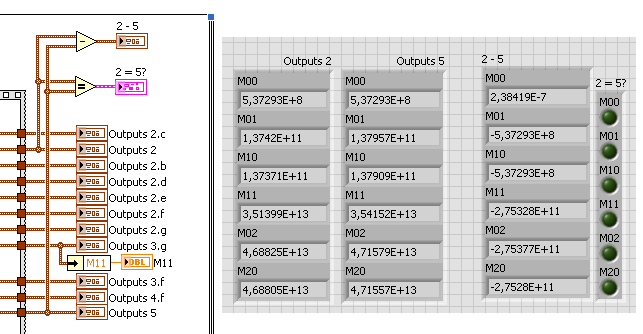
If you use an "Equal?" function and compare the new code with the old, the values are not the same. Only M00 is equal when all values are 4095.

Random numbers give slight different results.

Could you please take another look at it?

I'm planning to post my eventual code here. Calculate the Centroid and angle Alpha of an Image.

[johnsold]

Heinen,

Are you comparing the SGL values to the DBL values or the two algorithms with the same data representations?

How big are the differences?

Lynn

[GregSands]

No I didn't buy it -- I am a IEEE member and have access to the paper.

The numbers are the same for a starting index of 1.  In fact, this seems to be the preferred option anyway - otherwise you're essentially discarding one row and column of your image.  I did check for both 4095 and random arrays, also for a non-square array, so hopefully it is all correct.

What I didn't do was to fully credit the algorithm in the code - perhaps you could do that.

[SectorEffector]

Hello johnsold & GregS,

De comparison was done with all DBL.

What am I doing wrong?