- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How can I remove noise from a signal?
Solved!09-09-2011 09:04 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi everyone,
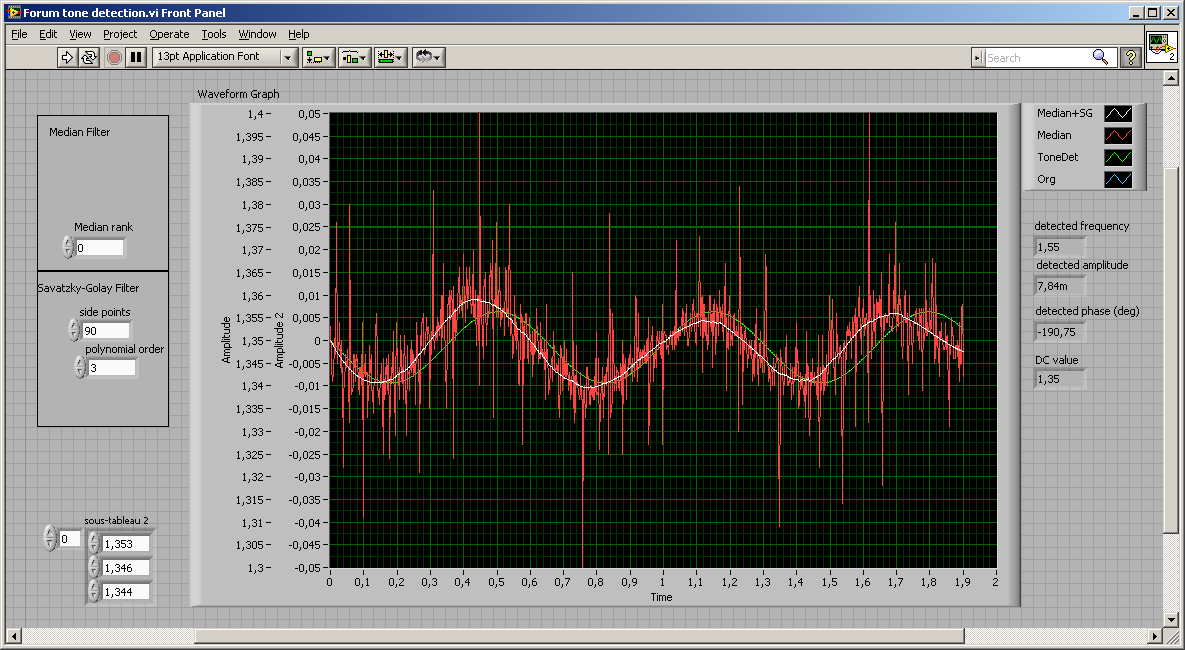
I need to extract the max and phase of a 1.5 Hz signal that has some noise (see attached files). I have been recording the signal at 500Hz. I am using the Labview filter tool set to "smoothing" with a factor set to 3. Could anyone tell me if am using the correct tool for what I want to do?. If so, is 3 a retativaly correct number? Looking at the result the signal is much better.
Thanks,
User
Solved! Go to Solution.
09-09-2011 09:45 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
It would be helpful if you saved your VI with some typical data. After you run the VI and get something like the image you posted, Edit >> Make Current Vaules Default (not sure what the French equivalent is), then save.
Smoothing filters are helpful at reducing noise. Your signal has some very high amplitude noise, relative to the signal amplitude. It will be difficult for any filter to remove that without significantly modifying your signal.
Other issues: All filters introduce some phase shift. You will need to detemine the amount of phase shift at the frequencies of interest and compensate your measurements.
What is the actual waveform of the noiseless signal? From your image I cannot tell if it is sinusoidal, triangular, or whether some of the "waviness" at the 0.005 amplitude level is part of the signal. What is the timing reference for the phase measurement?
Lynn
09-12-2011 02:39 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Lynn,
Thanks for your help.I Yes, forgot to save the default values of the array (see new VI).
I do need to extract the phase of the signal, but I already get a correct value of the phase when using the orginal noisy signal. Cleaning up the signal would enable me toget the max and min of the signal.
It is a kind of sin wave. The time reference of the signal is another signal, a square one that I measure in parallele of this one.
When using the Smoothing VI with factor=3 I have just realized that the first figures of the filtered signal are close to zero because the average starts with 0 values for the first one . Since I need to get the Min value (and the max) this is a problem for me because I don't get the right Min.
I could make up a smooth Vi my self, in which the average would only start after sample 3 but I am sure there is another kind of filter available in labview suitable for my signal.
I am not familiar at all with filtering a noisy signal after measuring it, from a software post treatment I mean,so I would like to learn on this example (without doing any "hardware" changes)
Would you know what kind of filter could be suitable in Labview?
Thanks
User
09-12-2011 04:37 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
here is a solution with the tone detection vi
to get better results:
If the frequence is known you can use a linear fit on a*sin(w*t)+b*cos(w*t)+c
Use more data
Improve the signal to noise ratio 😉
Henrik
LV since v3.1
“ground” is a convenient fantasy
'˙˙˙˙uıɐƃɐ lɐıp puɐ °06 ǝuoɥd ɹnoʎ uɹnʇ ǝsɐǝld 'ʎɹɐuıƃɐɯı sı pǝlɐıp ǝʌɐɥ noʎ ɹǝqɯnu ǝɥʇ'
09-12-2011 06:10 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Henrik,
I can't use more data because It'll make my test too long.
Would you mind explaining just a bit, how to use the linear fit if I know the W parameter ?
I will try your first solution in my next test.
Thanks you very much.
User
09-12-2011 06:16 AM - edited 09-12-2011 06:24 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
here some more to play 🙂
I didn't use the ordinary filter , however as more as you know about the original signal, as better your filter or fitting can be.
If you know it should be a sine (maybe even with a constant freq) and you want the phase , go with tone detection or a linear fit..
the median filter is good against spikes, the SG filter will do a polynominal fit (original designed for spectra fit but is also nice against noise with propper parameters
Uups, the pic was taken with no median filter ....:)
If you tell us more about the signal we might propose better filter. And keep in mind that most filter have an influence on the phase of your signal (phase/group delay).
Henrik
LV since v3.1
“ground” is a convenient fantasy
'˙˙˙˙uıɐƃɐ lɐıp puɐ °06 ǝuoɥd ɹnoʎ uɹnʇ ǝsɐǝld 'ʎɹɐuıƃɐɯı sı pǝlɐıp ǝʌɐɥ noʎ ɹǝqɯnu ǝɥʇ'
09-12-2011 07:25 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
If you are going to do data fitting, I would highly recommend you NOT filter beforehand. The data fitting is the filter. Also, given the noise on your data, you may want to consider something besides a least-squares fit. Before you do so, you need to answer the question of what type of noise you have. If it is random gaussian noise, then a least squares will do a good job for you. If it is something else, try a more robust fitting method. Check out the Numerical Recipes books for a good exposition on fitting techniques (check out Chapter 15).
09-15-2011 04:51 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Henryk I have run a test (long…) using the smoothing labview tool of my first post and adapted the array of data so that it doesn’t start with zeros (no average for the first value, average of the first 2 values for second one, first 3 for the third one, until I reach the value of the parameter in the Labview vi). The results are much better and enable me to make some conclusions about the test it self.
I didn’t use the Ton Detection because it really changes the aspect of my signal, and creates a “perfect” aspect of sin… I will perhaps want to use other things than the max or the Max-Min (for example the RMS) so I don’t want to be too far from the original signal (which is kind of "finger print").
I have compared on the chart your Median+SG solution to my smooth solution. They seem quite close, accept that yours reduces far more noise than mine. I will add your solution to my next test and compare both solutions.
Thanks for your time.
Thanks for your help and advice DFGray, I know I should take some time for studying filters.
User