- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Fitting two xy sequences of data
02-02-2019 05:25 AM - edited 02-02-2019 05:42 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
Can anyone help me figure out how to align to set of x,y data points.
These are extracted from a contour in an image.
The template sequence is the contour of the "ideal" sequence and sample sequence is from a contour containing flaws.
Todo:
1. Fit the sample set sequence to to the template sequence
2. Translate all points in the sample set to the template set (offset). So the curves are aligned
3. Measure the distance between the points
It can be done using image analysis in VDM but it is to slow and I need a mathematical approach.
The VI attached contains an example of the data sets to align/match.
Thanks
Certified LabVIEW Architect
CIM A/S
- Tags:
- fit xy align math
02-02-2019 06:04 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I don't have a solution, but some advice:
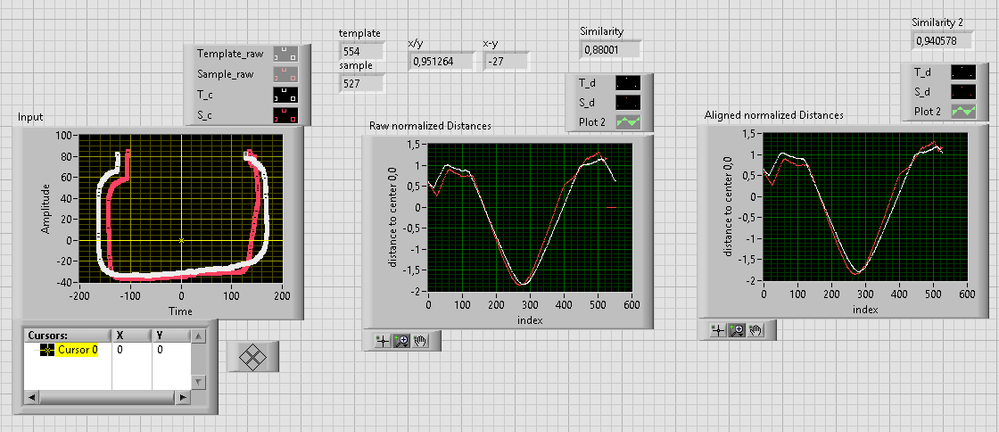
I'd work with distances based on centered x,y coordinates,
because then you can compare the Template and Sample as 1d arrays
e.g. to calculate a Similarity Quotient
The problem is still to scale the 527 sample data points to the 554 template data points.
I'd say there is no general algorithm to do this.
In this particular case it looks like you can simply cutoff the missing 27 data points of the Template Dataset:
This could be a (happy) coincidence!
By the way:
I normalize the distances just to visualize, why I think it is valid to cutoff the last 27 Template data points in this particular case.
To calculate a Similarity Quotient, I divide the sum of the sample distances by the sum of the template distances
Regards,
Alex
02-03-2019 02:08 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Alex,
Thank You.
Seems to be a good approach.
Will You share the VI ?
Certified LabVIEW Architect
CIM A/S
02-04-2019 07:21 AM - edited 02-04-2019 07:27 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@Kahr wrote:
Hi Alex,
Thank You.
Seems to be a good approach.
Will You share the VI ?
Yes, but I have the code on a different computer - and I want to polish a bit before uploading to the forums.
It's a bit spaghetti'ish, as you will need a separate For-Loop for each Dataset, as the number of datapoints is different
(template = 554 sample = 527, if you do both in one For-loop, the loop will stop at 527)
Is there a rational e.g. empirical reason for the difference between template and sample?
To my calibrated eyes, it looks like there's some kind of systematic bias
Is the sample number of datapoints always smaller or equal to the template number of datapoints?
Can you share some more sample datasets?
for both datasets:
1# calculate the arithmetic mean separately for the x- and the y coordinate
2# subtract the mean(x,y) from the Dataset(x,y)
--> this will center both datasets around the point (0,0)
3# Calculate the Euclidean Distance d between each Dataset Point (xi,yi) and the Center (0,0)
e.g. di = square-root(xi²+yi²)
--> this will transform your 2d Data to 1d Data
4# sum the distances separatly, and divded sum_sample/sum_template
Regards,
Alex
02-04-2019 07:34 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Alex,
I really appreciate it.
I've been working with a slightly different approach but getting to nearly same result for the alignment.
Looking forward to seeing the methods You are using.
I produce a lot of spaghetti for POCs (as CLA). So don't mind (;
Thank You
Certified LabVIEW Architect
CIM A/S
02-04-2019 07:50 AM - edited 02-04-2019 07:51 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Is there a rational e.g. empirical reason for the difference between template and sample?
To my calibrated eyes, it looks like there's some kind of systematic bias
Is the sample number of datapoints always smaller or equal to the template number of datapoints?
Can you share some more sample datasets?
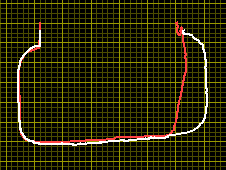
Yes. Actually it is the contour of a good and bad glass finger flange in profile. See attached image.
That explains both offset and potential rotation.
So the number of data points will vary and the method should take this into account.
I have attached another sample data set (just reversed).
Certified LabVIEW Architect
CIM A/S
02-04-2019 02:37 PM - edited 02-04-2019 02:46 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
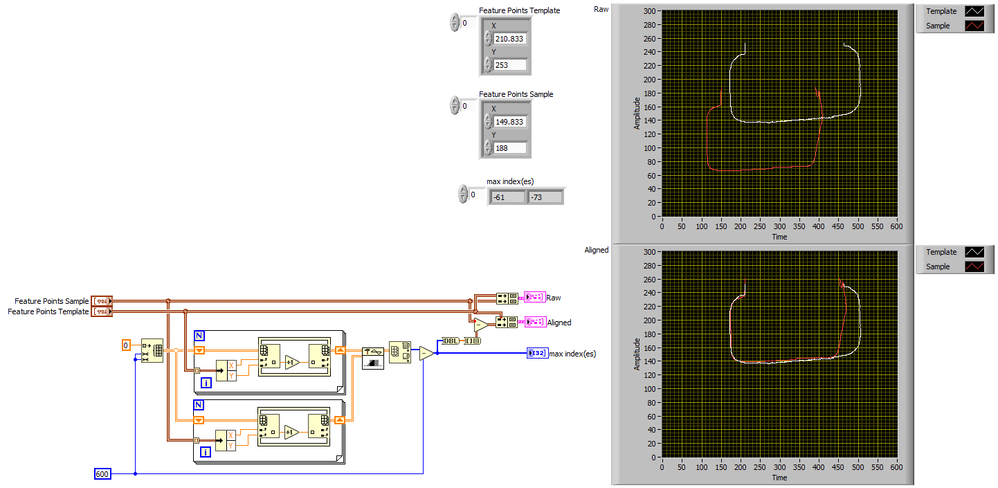
for both datasets, separately:
1# calculate the arithmetic mean separately for the x- and the y coordinate
2# subtract the mean(x,y) from the Dataset(x,y)
--> this will center both datasets around the point (0,0)
3# Calculate the Euclidean Distance d between each Dataset Point (xi,yi) and the Center (0,0)
e.g. di = square-root(xi²+yi²)
--> this will transform your 2d Data to 1d Data
4# sum the distances separatly, and divded sum_sample/sum_template
attached converted to a 2014 .vi
@Kahr wrote:
produce a lot of spaghetti for POCs (as CLA). So don't mind (;
the CLAD's natural inferior complex 😉
@Kahr wrote:
Looking forward to seeing the methods You are using.
produce a lot of spaghetti for POCs (as CLA). So don't mind (;
further information about this:
http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/OWENS/LECT2/node3.html
you might as well be interested in the LabView stock example
"..\National Instruments\LabVIEW 2018\examples\Graphics and Sound\2D Picture Control\Rotating a Picture.vi"
02-04-2019 02:45 PM - edited 02-04-2019 03:02 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@Kahr wrote:
Is there a rational e.g. empirical reason for the difference between template and sample?
To my calibrated eyes, it looks like there's some kind of systematic bias
Is the sample number of datapoints always smaller or equal to the template number of datapoints?
Can you share some more sample datasets?
Yes. Actually it is the contour of a good and bad glass finger flange in profile. See attached image.
That explains both offset and potential rotation.
So the number of data points will vary and the method should take this into account.
I have attached another sample data set (just reversed).
I think this is a feasible task, but not as easy as it might look at the first glance.
I'd say, the real word position of the scanned glass finger flanges must be rather stable for this method to work.
how are these "real world objects" transported in the active area of the camera?
Interesting idea to do a cross-correlation with the derived 1d arrays!
Align Feature Points.png 286 KB
What's an "angle map"?
This sound like the direction of the vector between image object datapoint and the center 0,0
So the length of such an vector would be what I named "distance"
02-04-2019 06:58 PM - edited 02-04-2019 08:43 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@alexderjuengere wrote:
Interesting idea to do a cross-correlation with the derived 1d arrays!
Of course you could map the data into 2D arrays and do a 2D cross correlation directly. 😉
02-04-2019 07:28 PM - edited 02-04-2019 08:44 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Note that my solution gives great fidelity in the entire left 80% where the curves are very similar and ignores the right side where they differ in shape. This is probably desired behavior. 🙂