- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
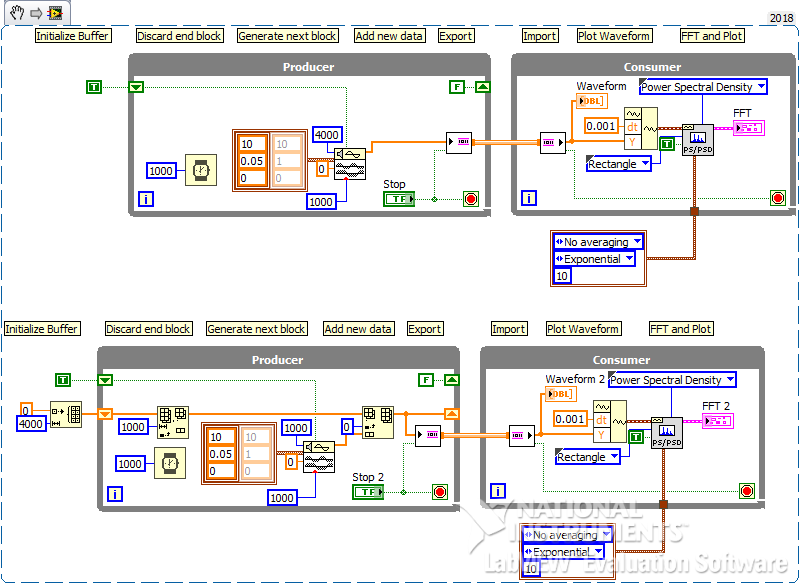
Continuous Power spectrum density at 0.25 Hz resolution
Solved!09-15-2018 12:29 AM - edited 09-15-2018 12:33 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks everyone for your help and replies.
@mcduff, you have used Hanning window, thus you are not getting -Inf values in-between.
Please check output with following parameters,
(i) Single AC input, any integer frequency (10 or 11Hz)
(ii) No noise & No offset
(iii) No window
(iv) PSD output
@Bob_Schor, actually I am using LV18, just that users with previous version can check attached VIs, i converted into LV12.
Please check output with aforementioned parameters. You will get -Inf results in-between.
For better clarity, I have attached snippet with output from both (expected and actual),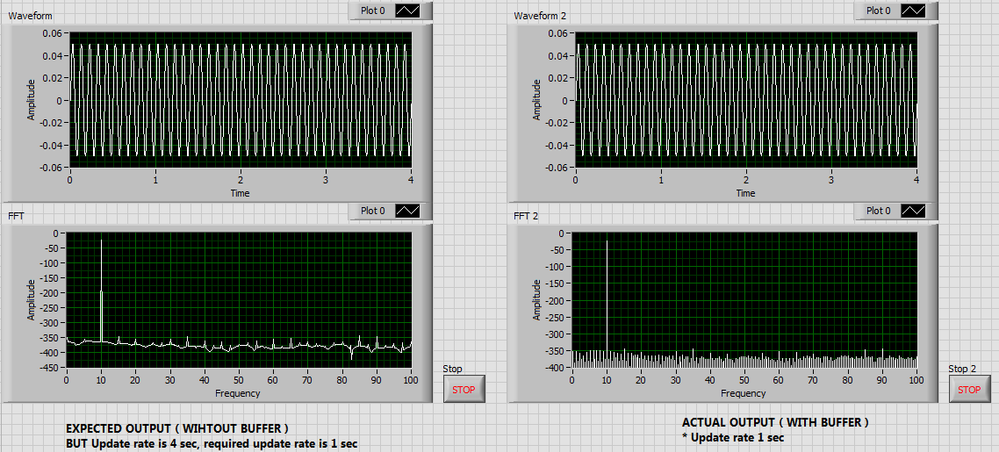
Please correct me if I am wrong. I think, data is not buffered in proper sequence.
I am assuming, output of Signal generator will be t0 to t999. So after 4 seconds, output after insert into array will be t3000 .. t3999.. t2000 . t2999..t1000 .. t1999 .. t0 .. t999.
But correct sequence should be t0 .. t999.. t1000..t1999.. t2000..t2999..t3000..t3999.
I didn't rectify array logic because, (i) as I have already implemented logic in reverse fashion in my actual (whole application), deleting element from 0 to 999 and inserting elements at last using build array and
(ii) because i am testing for integer number of cycles, hence incorrect sequence is not affecting the result.
(iii) I found out this observation, while writing down this reply.
09-15-2018 04:08 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
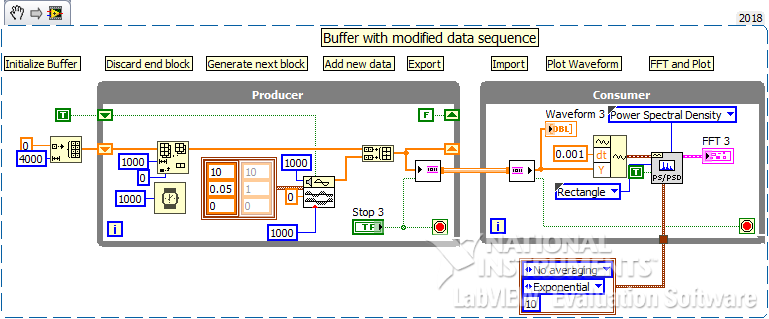
Please ignore my excuses to provide modified buffering logic, in previous post . As per my understanding, buffering should be done like this snippet.
I am deleting elements from start and inserting new elements at end. In any case, output of PSD still goes to -Inf.
09-15-2018 12:35 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Ouch! What a stupid mistake I made (and, as tired as he was, RavensFan hit on the fact I was building my arrays backwards -- delete from the front, add on to the back. Let me see if I have that available here, and try it out ...
Yep, it works just fine.
But I can 100% explain the -inf in your graph -- your signal is too clean! Notice the Boolean "True" in your PS/PSD function -- it means "Express in dB". Without noise, many of the components are 0, and what is the log of 0? Yes, -inf ...
Bob Schor
09-15-2018 12:36 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Just guessing here:
You are creating a noiseless signal, ie, a near perfect sine wave. The Fourier Transform of a sin wave is a delta function, that is 0 everywhere except at its frequency. You are looking at the PSD, which is the log of the power spectrum, Log[0] goes to minus infinity.
Stopped writing, BS beat me to it.
mcduff
09-16-2018 01:32 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks, @bob_schor and @mcduff.
Now I understand reason for -Inf values, but then..
1) If it's pure signal (without noise), then why do we see vertical lines @12, 13, 14hz...? That also shouldn't be there.
2) Same noiseless signal is provided in case of 'Expected output' as a chunk of 4 seconds @ every 4 seconds, but it doesn't give -Inf values, why? what's the major difference between Expected and Actual?
I hope, I am not stretching this issue very much. Please let me know, if I am doing the same.
09-16-2018 04:59 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Well, I, for one, cannot explain it, but largely because I can't reproduce it. I took my code, fixed my stupid error, added in the "dB" setting on the PS, used the settings (I recommend that you learn about Windowing -- there is a reason that Rectangular Windows are rarely used, and Hanning is the default value) you employed, and I still do not get -inf. The only difference is I'm running in a VM on my laptop -- I'll try it on my desktop (not in a VM) next week ...
Note that if you are going to use a dB scale, it may have a tendency (if you autoscale Y) to de-emphasize the peaks (which is where the "data of interest" lie). Maybe turn off auto-scale and set "something reasonable" for Y.
Bob Schor
09-16-2018 06:50 AM - edited 09-16-2018 06:52 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Actually, I am also running LV18 on VirtualBox.
For your testing, I have attached VI in LV18 version herewith. It is same as code snippets I have posted earlier.
09-16-2018 10:04 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Boy, this has been a "learning experience", I hope for you, but also for me, as I've made a few careless mistakes, and failed to spot the "obvious answers" until you "rubbed my nose in it".
So, admission, my code produces exactly the same results as yours, I just was "fooled" by the plot and therefore didn't come up with the "obvious answer" (as I had by pointing out that a value of 0, in dB, would be "-inf" if logarithms of 0 were allowed).
When you run your (or my) code, you see much of the plot sitting at -400 dB (which corresponds to a value around 10^(-40), a very small number). If you do not use the dB scale, it appears that the spectrum is 0 "almost everywhere" except at the frequencies in the signal (which, after all, is the "right" answer). Your "very reasonable question" is why, when you take dB, it isn't -inf "almost everywhere".
So here the final lesson, and the final part of the "solution" to your question (please, mark the Solutions so that other Community members interested in PSD computations "know" there are "answers" here). You are doing computations using floating point numbers, which are of finite precision. The computations involve computing sines and cosines, also involving finite precision, and arithmetic (addition, subtraction, multiplication, and division, or, as some have said, ambition, distraction, uglification, and derision). Although the correct answers should be 0, there will be round-off errors that might result in numbers very close to, but not exactly 0. That is what is happening here -- you can verify this for yourself by sending the values you are plotting to an ordinary indicator and looking at the array -- when I did this, every other number was 0, and in between were numbers with between 37 and 40 zeros after the decimal point (i.e. on the order of 10^(-40).
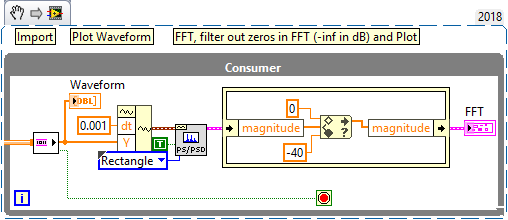
So here is a final piece of advice. Add a "Filter" to the output of the PSD to keep the range from going "off the deep end" to -inf. The attached Snippet shows one easy method -- take the points and "coerce" them to a reasonable data range. Since you expect the value to correspond to an amplitude of 0.05, depending on exactly what is being plotted, you expect a number on the order of 0.05 in dB, or around -20 dB. The nice thing is that now AutoScale Y works for you, and will let you see the peaks clearly.
Bob Schor
09-17-2018 09:35 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks Bob, that clarifies -Inf values. And also seems logical.
One query still remains, why isn't there -Inf values for 'Expected Output'.
I tried following with no success (i) enabling PSD only after 4 sec of data is gathered, with no success. (ii) generating timestamp for waveform at 4 seconds interval (iii) making 'restart averaging' TRUE before PSD starts.
09-17-2018 10:23 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@nik2013 wrote:
Thanks Bob, that clarifies -Inf values. And also seems logical.
One query still remains, why isn't there -Inf values for 'Expected Output'.
Please forgive me, but that's the "wrong question". Almost all of the values in Expected Output (as are almost all the values in the other outputs) -inf, except for rounding errors (note that -400 dB represents a value that is about as close as you can come to Floating Point Zero with a few low-order bits not quite cancelling out. If you do the "clipping" trick that fixed up the Actual Plots, you'd see that the "Expected" plots look the same.
So the right question is "Why does generating a 4000-point waveform all at once different from generating 4 identical sub-waveforms and concatenating them?". I honestly have no idea, but it could be that after 4000 iterations, the tiny rounding errors involved with adding dt to itself 4000 times "drifts" sufficiently to give the difference you are observing. I'd bet if you generated one 10Hz waveform with 100 points and replicated it 40 times (instead of 10-at-a-time replicated 4 times, or 40-at-a-time, replicated once) you'd get yet another result.
Make yourself a 72-point Bold Card that says "Floating Point Values Are Necessarily Approximations". Remember this when doing numerical computations. In particular, when doing comparisons of Floating Point values, never use "Is Equal", instead use "Absolute Value of Difference Is Less Than Or Equal To" and put in your "epsilon", a "precision" number that makes sense with respect to your problem, but is (a) positive and (b) non-zero.
Bob Schor