ni.com is currently experiencing unexpected issues.
Some services may be unavailable at this time.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Area between two curves/ lines
Solved!06-01-2018 11:35 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi everyone,
I have an accelerometer I am using to measure position of a thumb movement - this gets processed and spat out as a curve/line representing where the thumb moved in XY coordinates.
I want to then compare this to a 'target movement' vector, to see how far off achieving this target position users were when moving their thumb.
I have attached some examples of the actual movement (red) and desired movement (white dotted) lines. In the second pic of each example I shaded in white lines the area I want to estimate
Does anyone have any ideas of how they would implement this in LabVIEW?? I had thought about using integration and getting area under curves and subtracting one from the other, or turning the lines into a triangle and getting the area of the triangle (sometimes the lines are a bit curvey, but I don't mind losing some precision by making them into lines - rough estimation is good enough).
Thanks so much for any ideas in advance! I am new to labview and have crafted my life to avoid doing math generally, which now bites me in the butt
Solved! Go to Solution.
06-01-2018 12:07 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I'm going to question whether "area between curves" is what you really want to do here.
I would think you would want to plot/quantify "error versus time". If you set up your target trajectory to be "sampled" at the same rate as the actual, you could use the absolute value of the point-to-point distance at each time to show the error. The area under THAT curve might be what you're after.
Your data so far suggest linear movement and linear target. Could you quantify the error as angle and (final) distance error? That, of course, assumes all future tests will be linear.
06-01-2018 12:24 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hey there! thanks for replying
So are you suggesting that I take the data in a more raw form (i.e., I have it as acceleration in g's over samples - which I then later integrate once to get to velocity, then again to get to position). I use this data to get a root mean square value or something for the two different axes (X axis change, Y axis change), and then compare this with the target values for the same thing? That might work... though I would prefer to use the position data - as this is the feedback the users will actually *see*
Angles could work if I get nothing else to work, but I think it would miss some of the information out i.e., if there is a slight curve in the line, or its shorter than the target line etc. To get the angle I would use the dot product of 2 vectors to and cosine of the angle between these vectors I guess
If anyone thinks of anything that would be like root mean square but between these two lines that is also easy to implement in LV that would be brilliant 🙂
06-01-2018 12:32 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
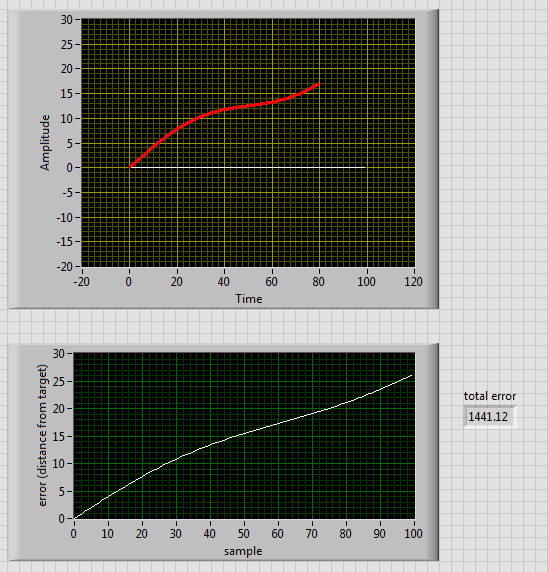
This is what the raw acceleration (g) data looks like
06-01-2018 12:53 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I think you might be asking the wrong question (or at least getting the math a little confused). In any behavior experiment, you need to ask "What is the goal?" (or what do you want the subject to do?). If the answer is "follow this target as closely as you can", one measure of "how good am I doing" could be "how close am I to the target". In the figures that you showed, what was curious is that the red line was in a different direction from the white line, so as time goes on ... Oops, my mistake (see next paragraph) ...
I just realized you are tracking a target in 2 dimension (X, Y), and there's an implicit third dimension of time. Disregard the emphasized word "direction" in the previous paragraph -- that was looking at the trace as an XY plot, when it is probably an X-t (or something else) plot. I'd be interested in seeing "closeness" vs t, as well as both delta-x (difference in X between target and subject) and delta-y vs t (to check for bias or spatial dependence).
Something that worries me a bit is using an accelerometer to measure the position of an object. You need to integrate the signal twice, and even an accelerometer at rest when integrated twice will show drift. [Probably a good thing I'm not reviewing this Project ...].
Bob Schor
06-01-2018 02:04 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I agree with Bob -- an accelerometer is probably the wrong tool to measure position. Be that as it may, even if you had perfect position data you still face the problem of quantifying the error relative to the ideal trajectory.
In my post I was suggesting comparing the position data at discrete points in time to get the 2D distance between them, not operating on the acceleration.

06-01-2018 02:31 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@Bob_Schor wrote:
Something that worries me a bit is using an accelerometer to measure the position of an object. You need to integrate the signal twice, and even an accelerometer at rest when integrated twice will show drift. [Probably a good thing I'm not reviewing this Project ...].
A lot of navigation systems actually do this. So it is not an uncommon thing. Granted, the good navigation systems also use GPS to retune the accelerometer and gyroscope tracking. GPS is slow, so not so good for many systems to rely on entirely.
There are only two ways to tell somebody thanks: Kudos and Marked Solutions
Unofficial Forum Rules and Guidelines
"Not that we are sufficient in ourselves to claim anything as coming from us, but our sufficiency is from God" - 2 Corinthians 3:5
06-01-2018 02:37 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
If memory serves me there was also a complication of a phase shift when integrating twice. Don't ask me to justify that math-wise. It is just something that I think I saw many years ago...
Ben
06-01-2018 02:45 PM - edited 06-01-2018 02:47 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@Zwired1 wrote:

Before Christian gets in on this action...
You might want to try messing around with Complex numbers since it does make the math a little easier.

There are only two ways to tell somebody thanks: Kudos and Marked Solutions
Unofficial Forum Rules and Guidelines
"Not that we are sufficient in ourselves to claim anything as coming from us, but our sufficiency is from God" - 2 Corinthians 3:5
06-29-2018 04:55 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks everyone for your suggestions, I ended up trying something that I think was a bit of a combination of your suggestions. I worked out the middle point (X,Y coords) and end point ('') of both lines, and then subtracted the absolute values to give a distance measure. The larger the distance the further away... not sure what people think of this approach...