BreakPoint

[ShotSimon]

Well I was going to let you come up with the maximum.  We know that there are 14 players sharing the time that normally 10 players would play.  So the maximum will be less than than 90 min per player.  Maybe on the order of say 90min - 90min/14

Regards,

-SS

[rpursley8]

A game has 900 man-minutes for 10 players.  Divide  that by 14 and get about 64 min and 16 sec per player.  This means you can rotate a player on the bench in every 6 min and 25 sec.  If you rotate them in the order you removed them, they should all play the same amount of time.

You can also follow the same pattern but rotate two players in every 12 min and 50 sec.

[ShotSimon]

rpursley8,

You are very very close to the solution.  How many players do you need to rotate and in what order, and how did you come up with 6min 25sec?

Are you able to demonstrate the solution in LabVIEW?

Thanks,

-SS

[rpursley8]

6 min and 25 sec is about 1/10 of the 64 min and 16 sec.  I'm sure I could do something in LabVIEW but I don't have the time to do it right now.

The players would be ordered like a circular buffer.  As new ones rotated in, the old ones would go to the end of the buffer.  the buffer has a size of 14 with the first 10 active and the last 4 inactive.

Message Edited by rpursley8 on 04-27-2010 08:37 AM

[ShotSimon]

rpurseley8,

Sorry I think you were close but I was looking for each player getting exactly the same playing time.  There are two valid solutions for 14 players given my rules. 

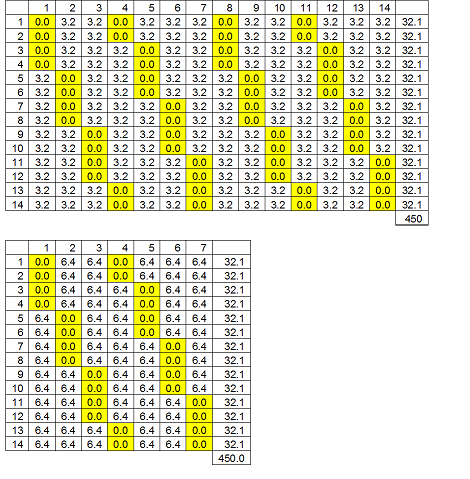
The simplest answer that I know for one half of a game is 45/14 ~= 3.2mins.  Four people will sub every 3.2mins.  There are a total of number of 14 substitutions, each player subs out four times.  You can also make 7 substitutions of 4 players, where each player subs out twos for ~= 6.4 mins.  You could also have solutions with 28 substitutions and higher at 1.6mins but the time intervals will get unrealistic fairly fast.

I did not deal with solutions that had unequal intervals but I am going to assume there are some.  You can change the number of players and see various solutions.  Although there is a magic constant equal to two that you will have to change to one to get the right solution.

Soccer may never be the same for all you LabVIEW users out there

-SS

Message Edited by ShotSimon on 05-03-2010 03:58 PM

Message Edited by ShotSimon on 05-03-2010 03:58 PM

[tst]

---

ShotSimon wrote: 

Soccer may never be the same for all you LabVIEW users out there

---

To which I can only reply with:

Kid: Doctor, will I be able to play the piano now that my cast is off?

Doctor: I don't see why not.

Kid: Good, because I didn't know how to play it before.

And before the soccer fans stone me, I should point out I'm not a fan of any professional sport (or is that just going to get more people worked up?   ).

[Intaris]

But what about time added on for time-wasting (Excessive substitutions)

Shane

[altenbach]

---

tst wrote: 

And before the soccer fans stone me, I should point out I'm not a fan of any professional sport (or is that just going to get more people worked up?   ).

---

 The only useful sport is the one you do yourself.

Also, there is nothing wrong with some forms of soccer, such as this.

 

[ShotSimon]

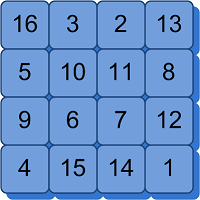
I'm in the middle of listening to Dan Brown's book, "The Lost Symbol".

He mentions a magic 4x4 square with some amazing properties, I won't give away all the properties since that in itself is something that you may want to discover for yourself.

 

So the Puzzle CHALLENGE is:  Using integers, positive or negative, I would like to know are there any other solutions that meet this criteria.  The normal magic square rules combined with the other "magic properties" for a 4x4.

If there aren't any (which I currently don't know if there are?) prove it with LabVIEW.

Lets keep the sum to between 0 and 999.  For example This Math site was kind enough to share the number of solutions with us given a Magic Total.

Regards,

-SS

[ShotSimon]

Just started reading a very large book called NKS by Steven Wolfram (A New Kind of Science).

It is an interesting book based around cellar automaton.  This graphical puzzle is simple but it's important you follow the rules.

First see this page:  http://www.wolframscience.com/nksonline/page-24

The Puzzle challenge - recreate the picture shown using LabVIEW allowing the initial condition do be configurable.

The first result is Blah, but changing the intial conditions to some of the other states is facinating.

-SS