Code Miniatures!

[John_P1]

Yeah, that crossed my mind too.  It would surely be optimal if you know how to achieve it.

Best Regards,

[altenbach]

I made a quick test doing diagonal scans (algorithm is actually quite simple but the elements are not fully sorted in size) and the advantage is typically not that great except for some cases (e.g. the size 14 is about 35 times faster but others are similar. Size 6 is about 30% faster). The triangle to be scanned is typically quite large in area, so the number of tests is not that much smaller.

A better approach might be to do my original search segmented, e.g. check all numbers that start with 9, and only go to numbers that start with 8 if the termination condition has not been met, etc.

[GregSands]

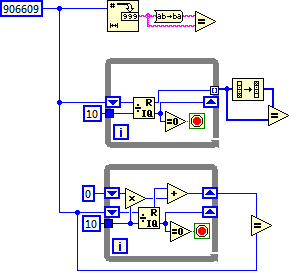
Interesting problem!  I managed to get my code down to 11 primitives + a few constants, slightly different to those previously shown (Palindrome3Digit.vi).  I didn't look at other code so I don't know how similar it is.  It checks 78 products on the way to finding the palindrome (on my computer 11.5us, or ~150ns per check, using I32s).

Side note: for me, the string comparison is as fast, or faster, at all sizes, than either comparing an array of digits, or a reversed number, as well as using the fewest primitives.

However, a quick check shows that there are actually 350 numbers greater than 906609 which are both (a) a product of two 3-digit numbers, and (b) a multiple of 11.

To be certain of having the correct solution, the code should check at least this many products, and I can't find a straight-forward way to rank them so that they are checked in strictly decreasing order.  So the minimum time should be in the order of at least 50us - unless someone has a faster way to check if a number is a palindrome.

I then looked at the larger problems (Palindrome.vi).  Observing the correct solutions allowed for generating a couple of heuristics which would guarantee finding the correct solutions for (at least) 2-8 digit numbers, but do so in a fairly small number of steps.  One gives a bound on the number of steps to try before moving to the next multiplier, and the other on a fixed lower bound based on the number of 9s present at the start of the largest palindromes.

[GregSands]

Of course after I post, I then come up with a much faster solution 🙂  The other obvious characteristic is that if the palindrome starts with a 9, it must end with a 9 as well.  That means that the last digits of the multipliers must be either 1x9, 3x3 or 7x7.  That greatly restricts the number of solutions that need to be checked.

So now for 3-digit multipliers, instead of starting with the largest multiple of 11 less than 1000 (990), we start with 979, and step this one down not by 11 at a time, but by 22, 44, 22, 22 (to give 957, 913, 891, 869 ...).  This also means that the other multiplier starts not at 999 every time, but at 991, 997, 993, 999, ... respectively, and drops not by the value of the first multiplier, but by 10x that value (to keep the last digit the same).

So, at the cost of one primitive and a couple of array constants, we only need to check 8 values, which is done in about 1.5us.

All bets are off if there is not a palindrome that starts with a 9, but that (heuristically i.e. hopefully!) looks unlikely.  I guess if you get down to values that start with 8, then the last digit must be 1, 2, 4 or 8, so that is again reduced.

For more digits, the first answers to check are those that end in 99, 999, 9999 etc, which gives scope for reducing the search substantially as well.

[altenbach]

Hmmm, just plugging my palindrome check subVI into your code speeds it all up by about 4x (~236ns total time versus 953ns for your code).

String comparisons are slower.

[GregSands]

Yes it works for >3 digits also (I did also find a bug in the earlier codes needing an extra Case Structure).  The times I get are (I64 solutions):

digits size time     checks solution

   2    04 220ns          1 9009
   3    06   4us         15 906609
   4    08   6us         23 99000099
   5    10  66us        200 9966006699
   6    12 700us       1864 999000000999
   7    14 191ms     455411 99956644665999
   8    16  92ms     182273 9999000000009999
   9    18  40s    73083091 999900665566009999 = 999920317 * 999980347

The code, with the required Case that should be in all the others too, is attached.

[GregSands]

Interesting.  I posted 3 palindrome checks that I'd tried:

 

Is yours different to any of these?  I found them all to be about the same, with the string comparison marginally fastest. For example, the other two slow the 16-digit palindrome check from 92ms to 109ms and 114ms respectively.  Besides my machine being slower than yours 🙂 what have I missed?

[altenbach]

(Posting by phone)
You know the number of iterations, so you could use a FOR loop. You can q&r by 1000 and only reverse 3 digits to compare with the other output. You could actually unroll the code and only compare the inner scalar pairs, the outer nines always match in your code. Etc...

[altenbach]

---

@GregSands wrote:

Yes it works for >3 digits also (I did also find a bug in the earlier codes needing an extra Case Structure).  The times I get are (I64 solutions):

digits size time     checks solution

   2    04 220ns          1 9009
   3    06   4us         15 906609
   4    08   6us         23 99000099
   5    10  66us        200 9966006699
   6    12 700us       1864 999000000999
   7    14 191ms     455411 99956644665999
   8    16  92ms     182273 9999000000009999
   9    18  40s    73083091 999900665566009999 = 999920317 * 999980347

The code, with the required Case that should be in all the others too, is attached.

---

See if this one is any faster. 😄 (Just a very rough draft, probably needs some cleanup...)

[altenbach]

OK, here's what I get:

digits size time   solution

   2    04    0ns   9009
   3    06    2us   906609
   4    08    2us   99000099
   5    10   22us   9966006699
   6    12  228us   999000000999
   7    14   63ms   99956644665999
   8    16   26ms   9999000000009999
   9    18    12s   999900665566009999 = 999920317 * 999980347

You need to be careful about folding. When we disable debugging, the outer FOR loop gets folded and we actually get a false result (single loop time/# of iterations).