- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Gaussian hypergeometric function 2F1(a,b;c;z)
Solved!09-09-2010 02:29 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
this is a somewhat specific question ![]()
I was very happy when I realized that the Advanced Analysis Library of CVI provides the Gaussian or ordinary hypergeometric function 2F1(a,b;c;z), GaussHG.
Unfortunately I have not been able to get the expected results, so I have to assume that I am doing something wrong and I would be grateful for assistance.
Here is the simple code trying to calculate the function
for ( index = 0;
index <= 1000;
index ++ )
{
x [ index ] = -10.0 + index * 0.0108;
y_1 [ index ] = GaussHG ( x [ index ], 0.5, 2.0, 1.5 );
}
The first 833 elements of the y_1 array yield NaNs, the following numbers are oscillating in the range from +0.57 ... +3.29
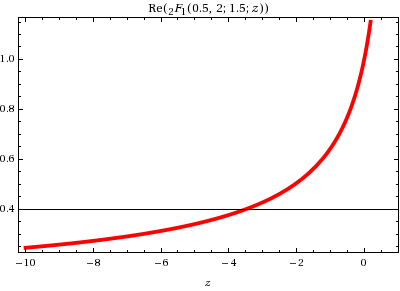
Here is what I would have expected, using the online function plotter from Wolfram Research:
Help is very much appreciated!
Thanks,
Wolfgang
Solved! Go to Solution.
09-10-2010 02:21 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello NI,
I have added some extra data to assist you in calrifying this issue, the data calculated by CVI are depeicted here:
As you can see, the function works reasonably only for not too negative x values. I would appreciate it a lot if this behaviour could be confirmed and fixed as soon as possible - I really need this function and do not want to implement it myself.
Thanks!
09-13-2010 01:25 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
for easier reproducing the issue I am attaching a simple demo project - would be nice to receive some feedback ![]()
09-14-2010 12:51 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Wolfgang,
I think this is a bug.
Thanks a lot for reporting this to us!
Joyce
09-14-2010 12:56 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi JoyceXe,
Thank you for addressing this topic. Sorry for being impatient this time but I need this function urgently. Is there a chance that you might provide a fix prior to CVI2010?? Otherwise I would need to implement it myself and obviously I'd like to avoid that... So please keep me updated about the progress with this issue. Thanks again,
Wolfgang
09-15-2010 04:58 AM - edited 09-15-2010 05:07 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Wolfgang,
We have reported this issue as a bug. For a quick workaround, I suggest you take advantage of the following transform:
F(a,b,c,x) = F(a, c - b, c, x/(x-1)) / (1-x)^a, which could map x from (-Inf, 0] to [0,1).
You could revise the original code a bit if performance is not a concern:
for ( index = 0;index <= 1000;index ++ )
{
x [ index ] = -10.0 + index * 0.0108;
if(x[ index ]>=0)
y_1 [ index ] = GaussHG ( x [ index ], 0.5, 2.0, 1.5 );
else //use the transform to map negative x value to [0,1)
y_1[ index ] = GaussHG ( x [ index ] / (x [ index ] - 1.0), 0.5, -0.5, 1.5 ) / pow(1.0-x [ index ], 0.5);
}
Hope this workaround could help. Please feel free to let us know if you have any more questions, thanks!
Arthur
09-15-2010 05:05 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Wolfgang,
We have reported this issue as a bug. For a quick workaround, I suggest you take advantage of the following transform:
F(a,b,c,x) = F(a, c - b, c, x/(x-1)) / (1-x)^a, which could map x from (-Inf, 0] to [0,1).
You could revise the original code a bit if performance is not a concern:
for ( index = 0;index <= 1000;index ++ )
{
x [ index ] = -10.0 + index * 0.0108;
if(x[ index ]>=0)
y_1 [ index ] = GaussHG ( x [ index ], 0.5, 2.0, 1.5 );
else //use the transform to map negative x value to [0,1)
y_1[ index ] = GaussHG ( x [ index ] / (x [ index ] - 1.0), 0.5, -0.5, 1.5 ) / pow(1.0-x [ index ], 0.5);
}
Hope this workaround could help. Please feel free to let us know if you have any more questions, thanks!
Arthur
09-15-2010 06:52 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Arthur,
Well, this workaround was a very nice surprise, thanks! Unfortunately, it is not yet fully working as expected, I got the following result:
As you can see, for negative x values the function now works as expected, but for x values from 0... ~0.4 still NaN are the result...
Of course, I could first probe x and then choose one of the two functions, the original or the transform, but this would make things quite slow (still much better than not working).
Thanks again,
Wolfgang
09-15-2010 10:55 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Wolfgang,
I guess you were using the transform when x>=0. However, we only use the transform when x is negative to avoid the bug(because x/(x-1) is positive). So the snippet I pasted actually probe x first and then choose between the original and the transform. I am sorry that will reduce the performance. But it is a quick workaround to get the correct result. We will try to investigate if there is other workaround to get both correctness and performance. Thanks!
Arthur
09-28-2010 06:42 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Arthur,
sorry for the late reply, I just returned from travel.
If I got you right you suggested using the original function for x=0 and positive x values. To me it seems that this approach does not give correct results.
For example, y=GaussHG (0.0, 0.5, 2.0, 1.5) returns y=8.948603854199588E-1, while I would have expected the result to be y=1.0, see here.
Accordingly, the function is not continuous at x=0, see the figure below:
Did I miss something? The above figure has been calculated according to your code snippet.
Thanks,
Wolfgang