From Saturday, Nov 23rd 7:00 PM CST - Sunday, Nov 24th 7:45 AM CST, ni.com will undergo system upgrades that may result in temporary service interruption.
We appreciate your patience as we improve our online experience.
Power Electronics Development Center
FPGA - Floating-Point math operations
You are absolutely correct. Single precision floating point overcomes most of the common numerical issues problems associated with fixed point math. Regarding FPGA space requirements, floating point algorithms can often be developed that take less space than the equivalent fixed point algorithm, provided that the floating point math operators are reused heavily. Typical embedded control applications run much much slower than the execution rate of floating point math operations. Therefore floating point math operators can be reused heavily.
Floating point algorithms also do not have the "brittleness problem" of fixed point algorithms. By brittleness I mean that fixed point IP cores can only produce the correct results within a limited set of conditions for which they are designed-- outside of those conditions they may produce an incorrect result. For example, if you assume an analog input will always be limited to a +/- 10 V range, but then someone decides to use the same IP core but scales to engineering units (i.e +/- 1000 Amps), then the fixed point algorithm may not perform correctly. It will only work within the constraints that the designer intended and tested for. In the control world, an incorrect numerical result should be considered a Fault condition, and should not be used to control a physical system. Therefore fixed point algorithms used in control should include code to check for numerical issues like overflow/underflow/saturation, etc.
By contrast, floating point algorithms are much more "universal" due to their ability to adapt to a wide range of signal dynamic range. There are still some numerical issues to consider such as:
1. The limits of math operations involving very small numbers and very large numbers (machine epsilon limits). For example, adding 1 to 16,777,217 should produce the result 16,777,218. In IEEE single precision floating point it results in the incorrect value of 16,777,217. In IEEE double precision, adding 1 to 9,007,199,254,740,992 gives the incorrect result.
2. IEEE floating point numerical operations that result in +Infinity, -Infinity, or Not A Number (NaN) which can be latched in forever if history or state is held in a feedback node or FPGA RAM buffer. That's because multiplying anything by Infinity either results in Inf, -Inf or NaN, and multiplying anything by NaN results in NaN. Therefore, those values can get "latched in forever" if you don't check for them. (In my opinion, it would be better if they didn't exist in the IEEE floating point standard.)
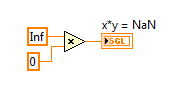
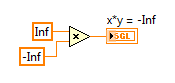
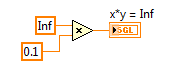
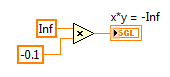
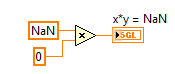
Here is an example of an Runge-Kutta 1 Backward Euler integrator which includes code to check for these conditions before storing the x
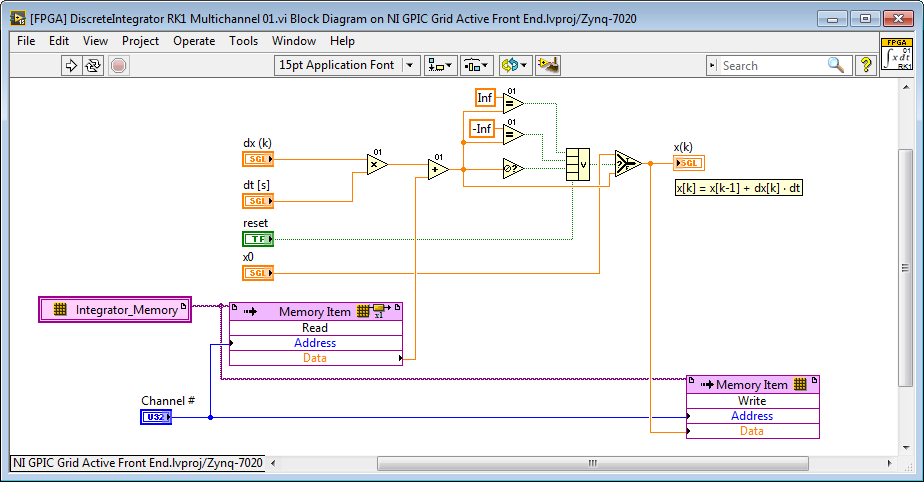
Regarding FPGA space requirements, floating point algorithms can often be developed that take less space than the equivalent fixed point algorithm, provided that the floating point math operators are reused heavily. My LabVIEW FPGA Floating Point Algorithm Engineering Toolkit is designed to make it easier to do that, but also contains high speed floating point operators for use inside Single Cycle Timed Loops that cannot be shared. See these application notes for details. Also, IP Builder provides a powerful way to create highly efficient, high speed floating point algorithms that share resources and also satisfy the latency (speed) requirements you specify.
Move Any Control Algorithm or Simulation Model to Embedded FPGA Hardware with New Floating Point Too...
Whitepaper: New ultra-fast, FPGA-based, floating-point tools for real-time power system simulation a...
For the latest version of the floating point toolkit and IP cores built using it, go here:
Guide to Power Electronics Control Application Examples and IP Cores for NI GPIC
Floating point will be used for almost all control IP cores and other algorithms that I develop in the future. There are only a few corner cases remaining in which fixed point math is still required.
It may be that you are using a slightly different Xilinx compileror LabVIEW version, or targetting a different FPGA target such as NI SOM. In those cases, regenerating the IP using the Xilinx Coregen blocks may be required. As you found, once you regenerate the IP it should be working fine. Also make sure that long directory paths is not causing the problem-- see this post.
By the way, for floating point math inside a single cycle timed loop (SCTL), I find IP Builder to be very powerful and more easy to use than the SCTL IP cores from the float toolkit. See the Proportional Resonant Controller with Multiple Harmonic Compensation developmental code here for a good example (unzip to short path). It only takes 441 ticks (11 microseconds) to execute PR controllers up to the 19th harmonic in floating point and could be even faster if needed. To achieve the same performance with the float toolkit SCTL IP cores is possible but would take a lot more work. It is nice to have the IP Builder high level synthesis tool do the work!
Note that for IP Builder FPGA RAM Access functions are not used. Instead, you use arrays which are automatically converted to FPGA RAM by IP Builder. Here is the Proportional Resonant Transfer Function Solver for IP Builder.
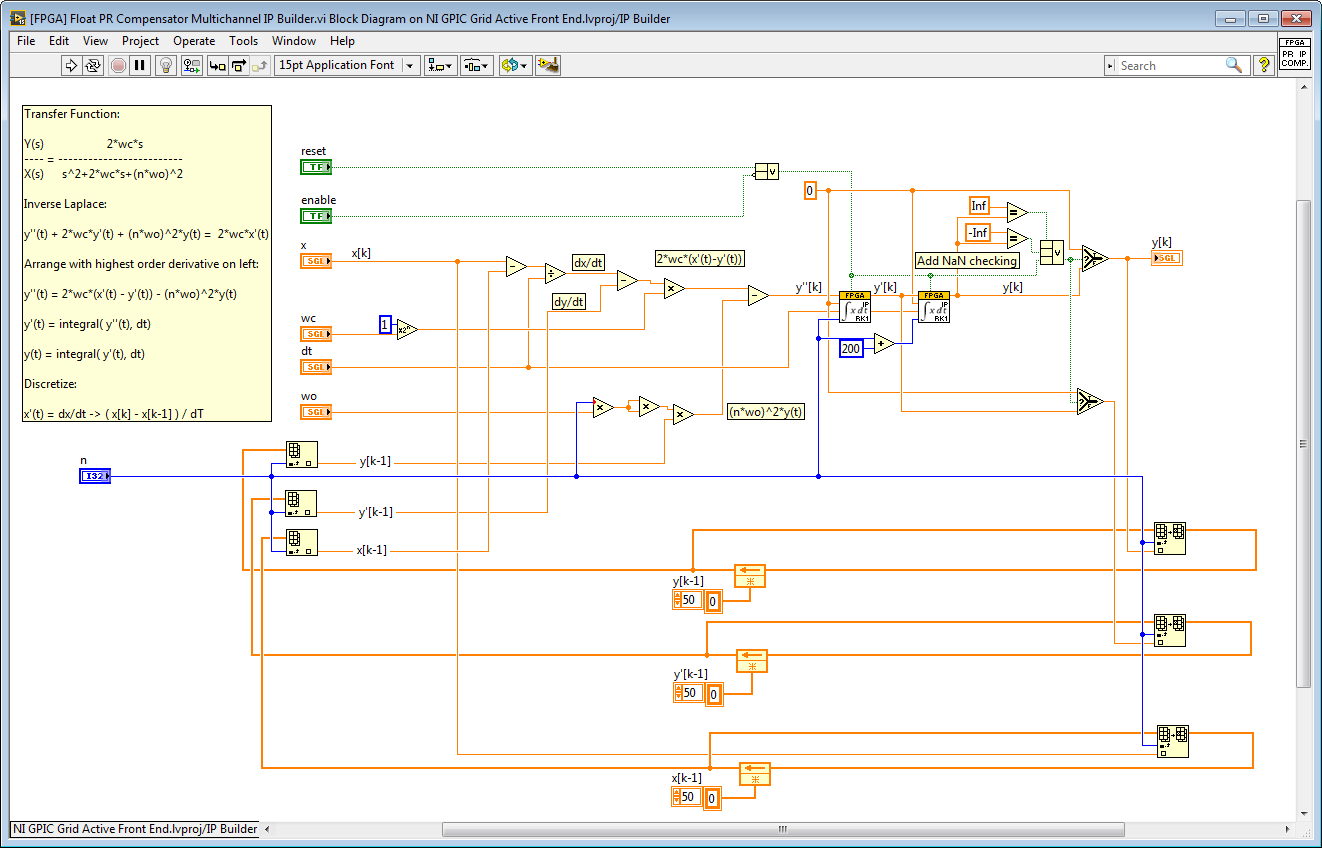
Transfer Function:
Y(s) 2*wc*s
---- = -------------------------------
X(s) s^2+2*wc*s+(n*wo)^2
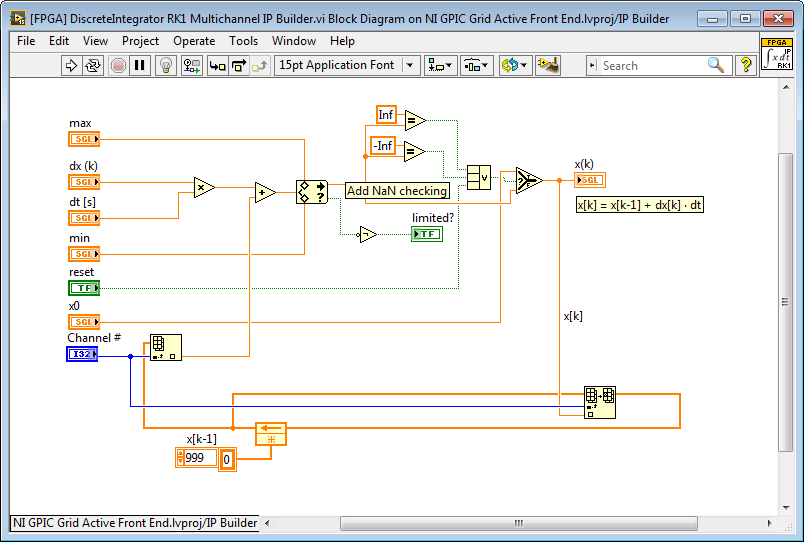
Here is the RK1 Multichannel Integrator Solver for IP Builder. Each harmonic frequency uses a different channel.
Here is the top level IP core, which sums the contribution from the PR Compensator for each harmonic. It has the structure shown in the block diagram image below but implements the non-ideal PR resonant controller.
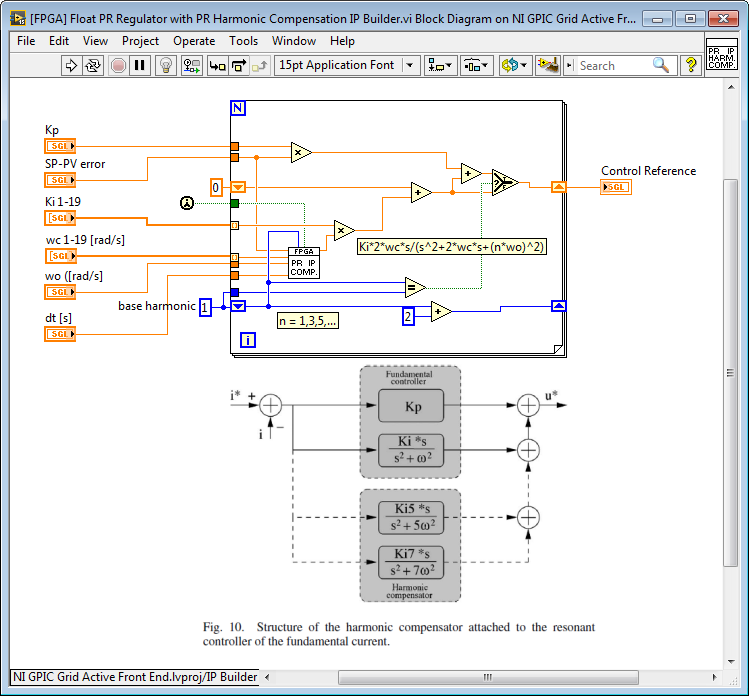
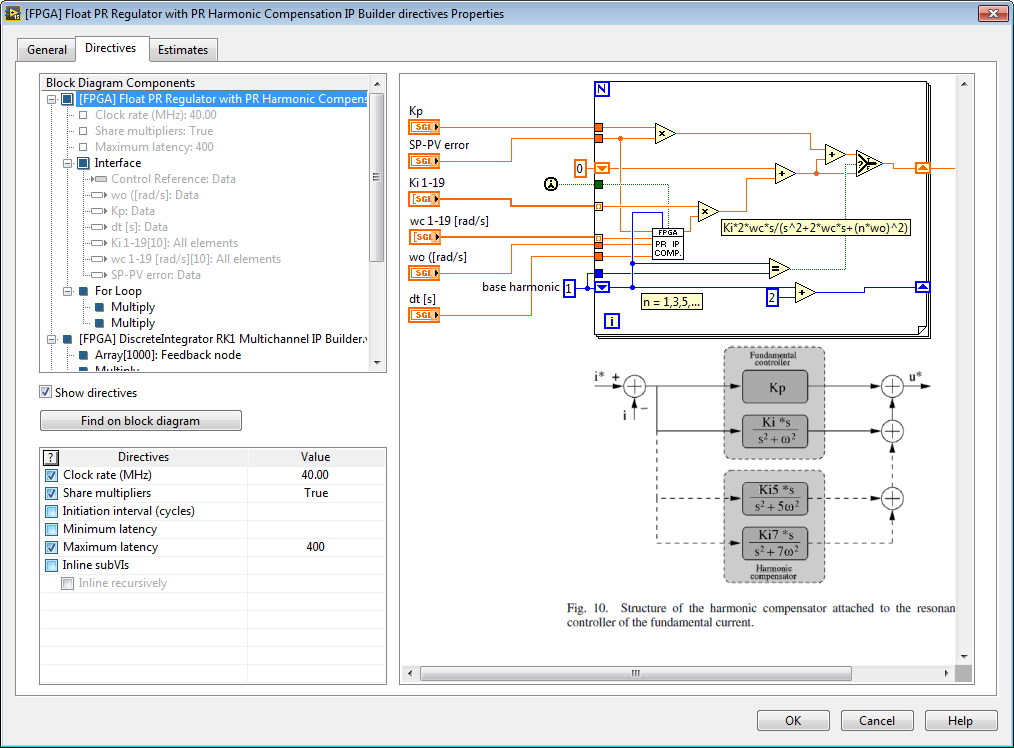
Here are the IP Builder Directives. By changing the settings, you can make it faster or reduce the amount of FPGA resources used. You can also estimate the resources used.
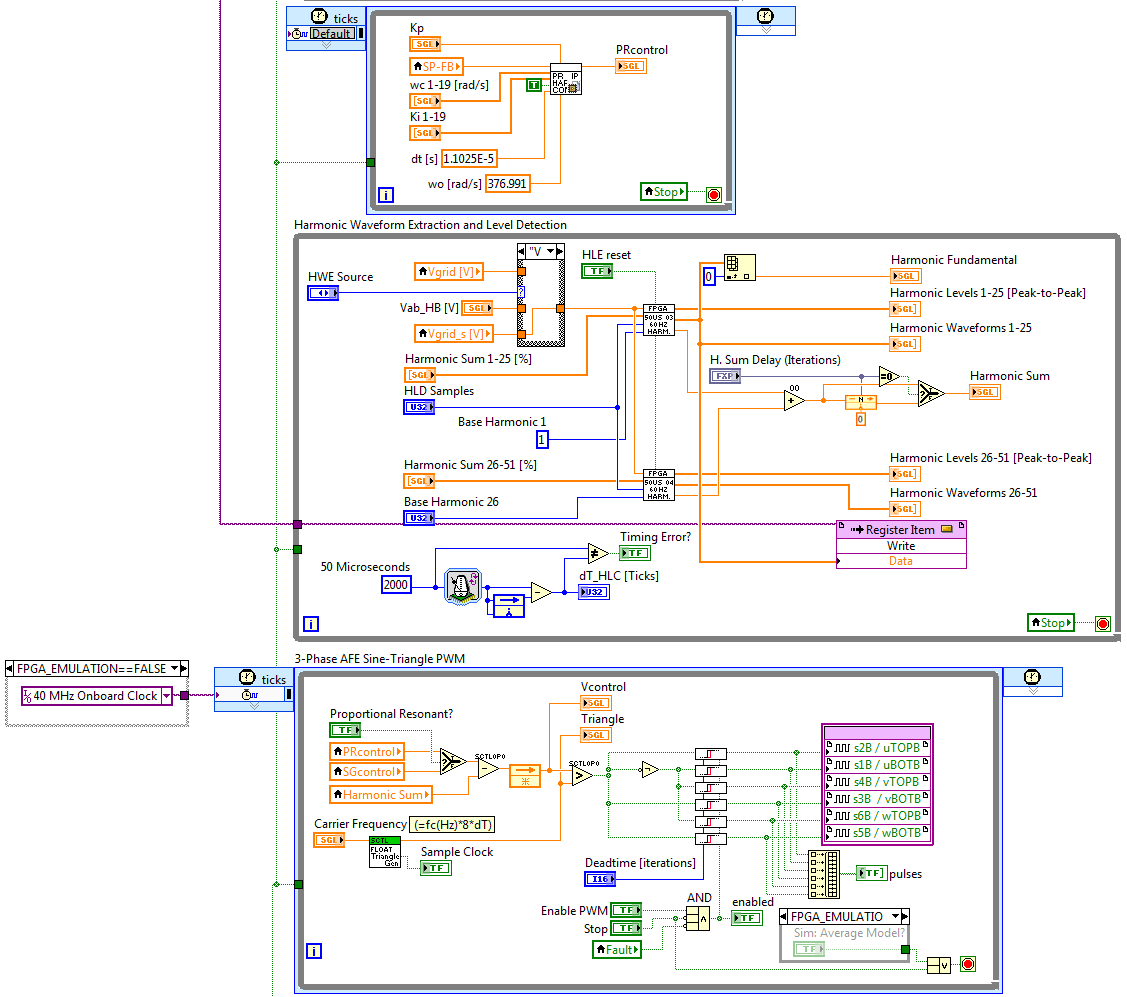
Here is the IP Core generated by IP Builder back in the main FPGA control application (the top loop below). Note that it runs inside a single cycle timed loop (SCTL), but only updates every 441 clock ticks.
