- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
automating subjective criteria: log graph with background noise
09-15-2016 09:33 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
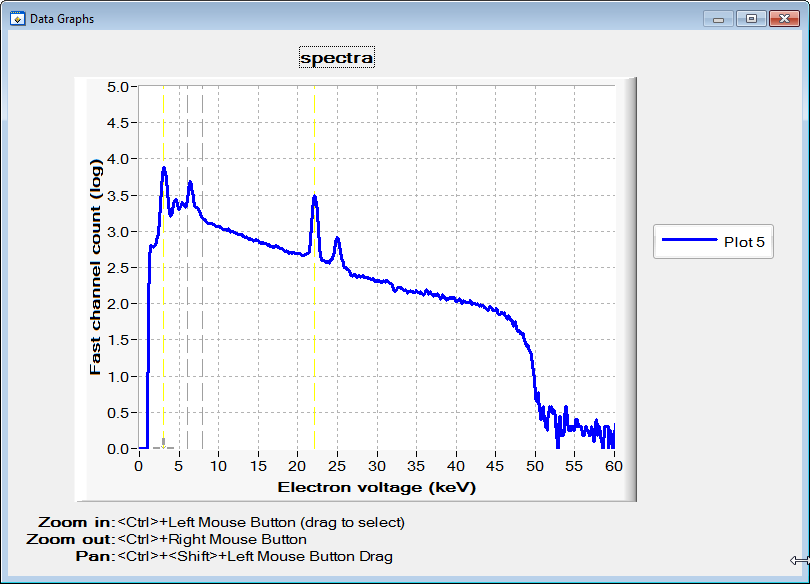
This is a bit obscure, but I have a challenge for you. I'm tasked with automating a step in a test, which currently is being done visually by the operator. It involves a count-rate plot on a graph control (a spectrum plot). The single criterion is to be sure that the cutoff occurs at 50.00 on the X-axis.
This is a bit tricky to isolate, due to the amount of noise after this spot on the axis. I tried looking at a polynomial trend line, but this isn't very helpful.
Thoughts?
09-15-2016 10:27 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
How is the "cutoff" defined?
IMESTEK
09-15-2016 10:31 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Have you considered using the Threshold function?
IMESTEK
09-15-2016 10:36 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
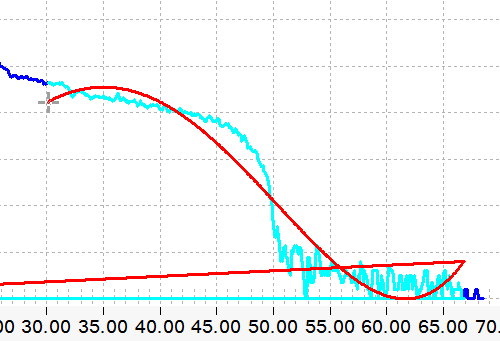
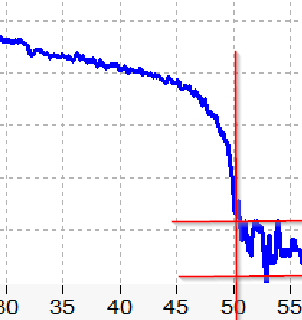
The spectrum must asymptotically approach 0 on the Y axis at 50 in the X. I've drawn some lines:
You can see how it's tricky, since the noise floor keeps the Y magnitude up near 0.5 at 50. A failing unit will look like this:
...where the "knee" of the curve begins slightly before (or after) the 50.0 point.
09-18-2016 05:26 PM - edited 09-18-2016 05:41 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I wonder if using the trend of the derivative function can be of help.
This could be preceded by some preprocessing like removal of outliers and possibily some averaging to smooth the function, if all that does not introduce relevant modifications to the phenomenon being studied.
Proud to use LW/CVI from 3.1 on.
My contributions to the Developer Community
________________________________________
If I have helped you, why not giving me a kudos?
09-21-2016 04:10 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
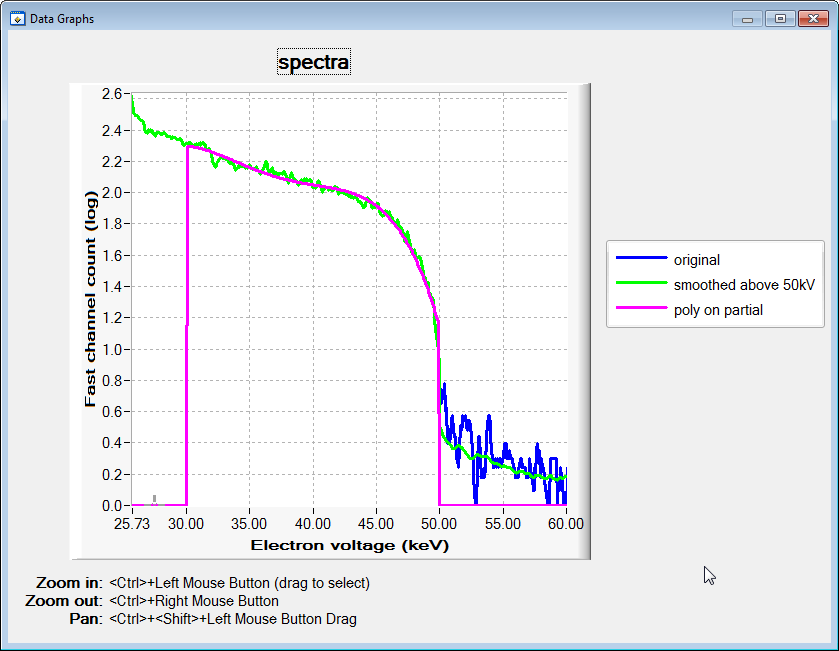
I'm making some headway. I first did a very broad smoothing of the plot above 50.00. This gave me:
I then cropped out a window of this data and did a poly fit:
My reasoning is that if this poly fit intersects near 50.00, I'm in range. We'll see...