relative min and max of xy-graph

[ManuelElze]

Hello,

I am really stuck and I need some help solving this issue.

I have different graphs and I need to find the relative minimum and maximum for further calculations in my program.

With some data, it is quite easy because the absolute and relative points are identical, but not always.

So far the user needs to manually interfere to get correct values with the difficult data.

Does anyone have a solution on how to always find the relative minimum and maximum points of the graph automatically?

I tried some weird calculations but none of them worked for all cases.

I attached a sample vi.

(the graphs will always be different but I think they won´t get worse than the second one)

Best regards

Manuel

[GerdW]

Hi Manuel,

What about searching for sign changes in the derivation of your signal?

This way you can find relative min/max points. Once you know all relative min/max points you can easily filter for the interesting ones…

[altenbach]

Peak detector with well, tuned inputs should do what you need.

Does the sloping "background" have a mathematical description? Maybe it can be subtracted first.

What else do you know about the datasets? Is there exactly one local minimum and local maximum or could there be more than one each?

(Be aware that solutions that depend on derivatives are quite sensitive to noise and might require filtering.)

[BertMcMahan]

I have done a similar task using cursors. The user drags a cursor near the peak, and when they let go the program tries to snap to the nearest local peak. When the plot cursor was released, I looked at something like 20% of the displayed plot and found the min or max within that window.

[altenbach]

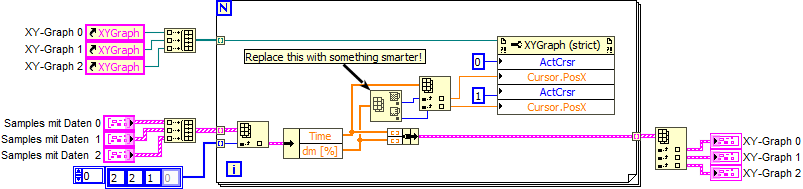
Since your new and improved algorithm needs to work an all three datasets, the first thing would be to eliminate all that duplicate code, e.g. as follows. Now all you need to do is change one small code section and immediately test it on all inputs. Having to do the same changes in three different places is error prone and tedious.

[ManuelElze]

Thanks for the replies.

I tried searching for sign changes in the derivation of the signal. But because I don´t have a mathematical description of the signal I have trouble filtering the right points.

The Peak detector doesn´t give me reliable peaks and valleys. For example, the second signal doesn't show any peaks with the detector (see image).

Using the cursor to drag to the nearest peak is exactly what I am doing at the moment and trying to avoid. But I think I need to use this method as a backup to manually correct the calculation in case it is wrong.

And thanks for cleaning up my code, but I have hundreds of different signals and I just copied some of the bad ones as examples.

[altenbach]

---

@ManuelElze wrote:

And thanks for cleaning up my code, but I have hundreds of different signals and I just copied some of the bad ones as examples.

---

It is more an attempt at a better test harness. Ultimately, the final algorithm should work for all possible signals and you can use it to e.g. iterate over all available datasets (i.e. put the file read inside the loop). It is conceivable that some of the datasets that currently work might fail with the improved algorithm. Testing is always important.

[altenbach]

---

@ManuelElze wrote:

Using the cursor to drag to the nearest peak is exactly what I am doing at the moment and trying to avoid. But I think I need to use this method as a backup to manually correct the calculation in case it is wrong.

---

Your curves had so few features that fitting to a sufficiently high polynomial should give you very good initial estimates of the peaks and valleys. To refine, you can follow that up with a second or third order polynomial of the surrounding point range. See how far you get.