enhanced Smith Predictor for modelled plant

[Barp]

Yeah... welcome to the 'art' of control. 🙂

There are several steps you need to secure to be able to 'match' different simulations and obtain the same response. Let me go one-by-one:

1. First, I looked back at the Smith PID structure. Actually, that structure is the academic (the gain multiplies the derivative and integral gain).

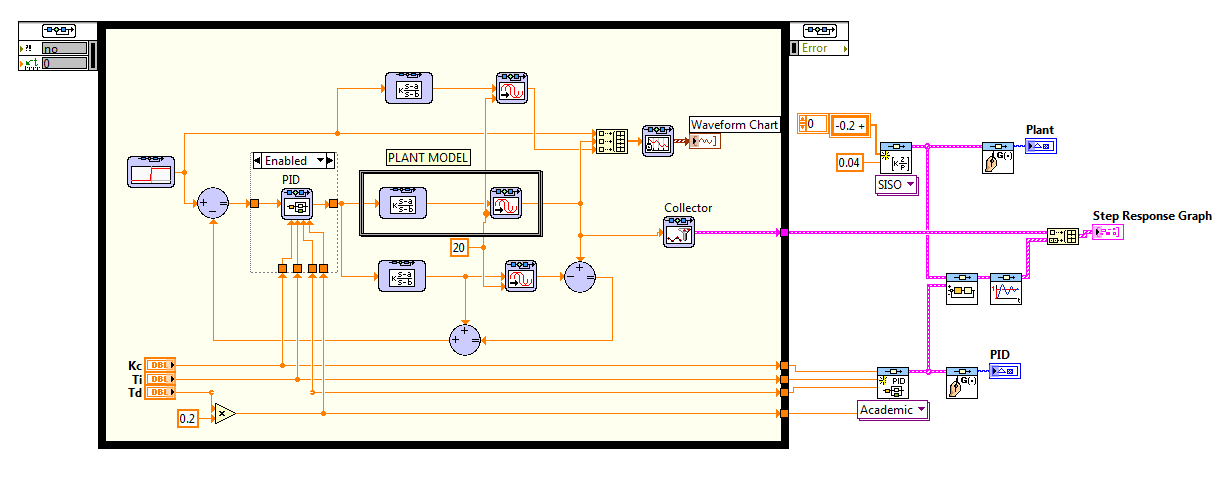
2. The plant I simulated was not the same you had. I used the same plant you had on your first post and I think you have a different plant. Here is what I have now:

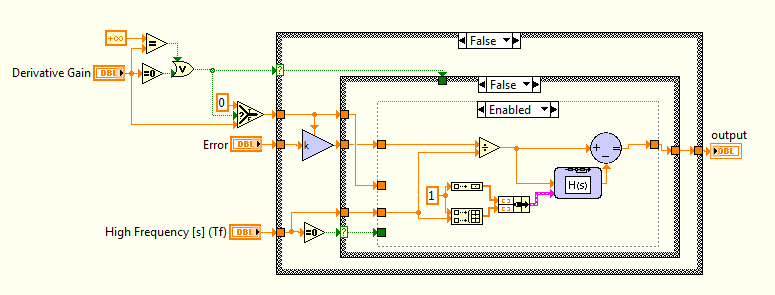
3. One of the main problems of usign PID algorithm is the how you implement the Derivative action. The Smith PID uses the 'derivative' block from SIM. Although this is ok in several implementations, you need to be careful that the results are compared with other implementations. In 2011 we added a PID block that implements the PID we have in Control Design. Both algorithms have 'Tf' parameters that adds a 'filter' for the derivative action and I used Tf = alpha*td to obtain this algorithm (alpha= 0.2). Here is the code that also compares with Control Design:

4. When I said to use the Unit Feedback, you don't need to use the series block. See the code above.

5. I also had to 'tight' the time response of the simulation to match the control design results to 0.01. Larger timestep will make the simulation different.

After all those changes, here is the result of the simulation. I added delay to the plant (20 s) to show that, independent of the delay, the response of the smith predictor is the same as the plant without the delay.

Hope this helps to clarify a lot of your questions...

[Barp]

PS: Since you have the LabVIEW Student Edition, I would strongly recommend you to update to LV 2012 SP1. There was several features and bug fixes that improved considerably the software. However, just in case you can't access it, here is the PID Implementation for derivative action:

[Remmix · Accepted solution]

Thanks Barp for the further clarifications.

Yeah right I also noticed that you have different plant to my original one. My plant has a Third Order Plus Delay (TOPD) model and I am using a PI controller (instead of PID). I then implement the Smith Predictor with the tuned PI controller parameters to control the plant. The plant 0.04 / (5s+1)^3 and so the resultant TF would be 0.04 / 125s^3 + 75s^2 + 15s^2 + 1.

I can see you actually have a good response from the graphs. The problem I am facing is I only have LV 2010 Stud Edition and do not have access to the PID functions you have.

Cheers,

Remmix

[bunnykins]

Hi Remmix,

I presume that you are working on the Industrial Case Studies module assignment for GCU ?  It is possible to implement this assignment using LabVIEW 2010 Student Edition (I did).

Regards,

[Remmix]

Hi Barp,

I was away with work since I last visited here but just wanted to say thanks for your help. I managed to resolve the LV codes.

Your input was very useful so cheers..

Kudos

Remmix 

[Barp]

Remmix,

Just to let you know, based on our discussion, I improved the shipping example that we have in the Control Design and Simulation Module.

Thank you for helping improving the product. I hope you keep enjoying it!