create a curve from points to get more values in labview 2021

[Ash-ta]

Hi everyone,

I'm using labview 2021,

I need some help with a dashboard project I'm working on. I want to read sensors (let's say a torque sensor for a rotating shaft), and to get the final results correctly I have to consider the loss in the torque. So I made a trial free run for the system and I got the resistance torque for several rotational speeds. For example, I have n1=200, n2=400, n3=600 rpm, and so on, and for each speed I have a resistance torque, Q1, Q2, Q3, ...

My question is how to use these values to create a curve that can help me to get the resistance torque for any speed I want. For example, how can I make a curve from the above data and then use it to find Q for n=300, not 200 or 400.

I was thinking to use a fitting node to smooth the values I have first.

Thank you for your help. Any suggestion can be useful because I don't really know which direction I should go through.

[JB]

In order for us to be able to help you efficiently, please indicate the values you have measured and the expected accuracy of the correction.

A linear or polynomial interpolation seems to be the solution.

[GerdW]

Hi Ash-ta,

---

@Ash-ta wrote:

So I made a trial free run for the system and I got the resistance torque for several rotational speeds. For example, I have n1=200, n2=400, n3=600 rpm, and so on, and for each speed I have a resistance torque, Q1, Q2, Q3, ...

My question is how to use these values to create a curve that can help me to get the resistance torque for any speed I want. For example, how can I make a curve from the above data and then use it to find Q for n=300, not 200 or 400.

---

So you have a list of X-Y pairs and you want to get a polynomial fit for them?

What about using the polynomial fitting function (Math->Fitting->PolynomialFit)?

It will output the polynomial coefficients: use them with the PolynomialEvaluation function to calculate your "resistance torque" for each "rotational speed"…

[Ash-ta]

Thank you for your answers,

@JB please take a look at the attached image, it has the values of n and Q, although the values of Q look roughly like linear but I want to take the chance of writing here to learn the general case of nonlinear application, 

@GerdW, do you mean like what I did in the attached Image?

I see the values are very far from the original table, for example, in the image I entered n= 0 and after the conversion it gave 1.188 which should be 0 based on the original table

[JB · Accepted solution]

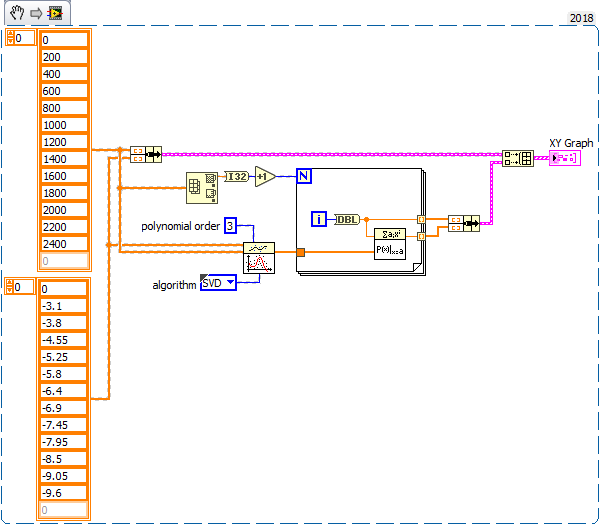
Example :

If no interpolation method reduces the error sufficiently, I would separate the signal into several parts (two should suffice) to interpolate them separately.

[Ash-ta]

---

@JB wrote:

If no interpolation method reduces the error sufficiently, I would separate the signal into several parts (two should suffice) to interpolate them separately.

---

Your example answered my question thank you, however can you please tell me more what do you mean by " interpolation methods", do you have any suggestion about reducing the error?

We can notice from the curve that the resistance torque changes fast between 0 and 200 rpm, then it continues more like linear.

Changing the polynomial order helped, but still not enough.

I care more about speed between 0 to 1600 rpm, and i mostly care about getting 0 torque for 0 rpm because logically we can't have resistance torque unless the machine is turning.

[GerdW · Accepted solution]

Hi Ash-ta,

play with all those options:

[JB]

To refine the interpolation, it would also be necessary to have additional points between 0 and 200rpm.

[JB]

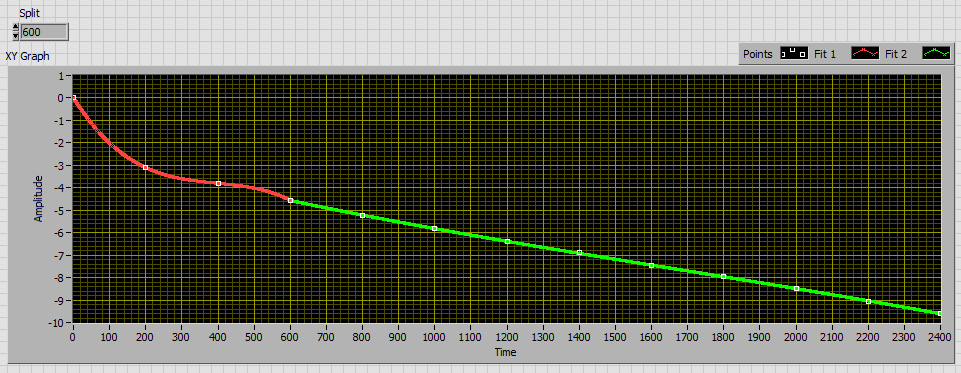
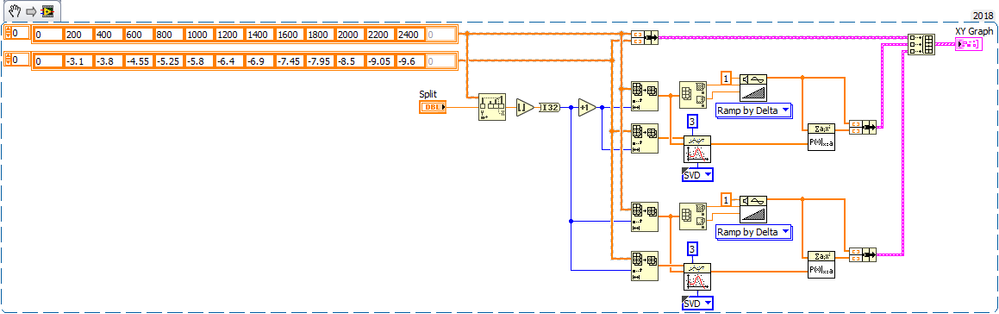
Here is an example of a polynomial fit by splitting the signal into two parts. As already mentioned, more points between 0 and 200 (400) rpm would be needed to get a better result in this area where the friction changes non-linearly.

It would then also be possible to lower the separation point of the signal and thus optimize the interpolation of its two parts.