can you costrain General Linear Fit VI?

[altenbach]

We are missing a subVI, but I don't think it is needed. How much noise is typically in the data?

I assume your example data is simulated. Does real data have other distortions and possibly trace components/impurities that are not in the matrix?

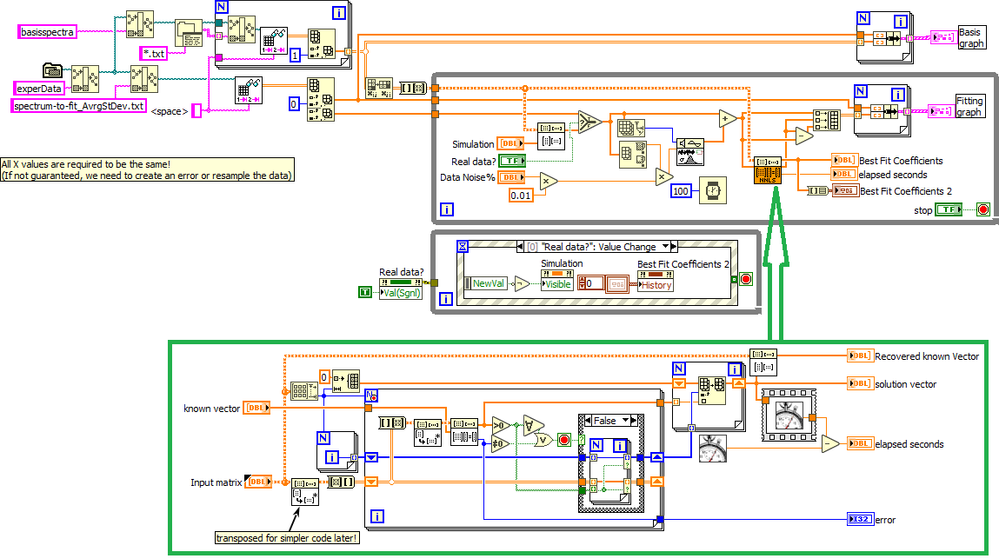
I wrote a small program that solves the linear system and iteratively eliminates the terms that give negative results from the H matrix until only positive terms remain, then fills them back as zeroes at the end. Seems to be about 500x faster than your current approach and gives the correct result unless there is a lot of noise. I have it on a different computer and can probably attach it later.

The way you read the data seems to be pure Rube Goldberg and you don't test if all the x-arrays are identical. An absolute requirement for the method to work, else you would need to resample all data to a common x-array.

[patriziocandeloro]

Dear Altenbach,

thanks for your prompt answer. I noticed that there was a missing subVI and I soon substituted the attached zip file.. maybe another one is missing, hopefully not important for testing, but I do not have computer with me now and I cannot upload a new zip file at the moment

About the X axis, in the main software I'm providing that it is the same for all curves, both basis curves and curves to be fitted.

The experimental curve to be fitted, that I uploaded for testing, is the average of two different groups of curves. Effectively the experimental noise of each single curve could be something like 5-10 times larger.

So far I tried to use a pseudoInverse approach to solve this algebra problem:

B*c=y

where B is the matrix of the basis curves, c is the array of desired coefficients, and y is the experimental curve to be fitted.

But with this approach I do not have any control on the range of c values (only positive values are desired) and I do not have any direct output assessing the goodness of the fit (covariance, correlation, other error estimation?)

kindr egards,

pat

[patriziocandeloro]

Dear Altenbach,

i doubled checked the subVIs and now there should be nothing missing in the .zip file.

All the best,

pat

[altenbach]

Even with your implementation, there is gigantic room for improvement because the fitting seems to fail with high probability.

• Never ever maximize the front panel and diagram to the screen. It is very hard to only look at one thing at a time. Currently you can't even look at the help while editing any of the diagrams!
• All analysis is done in DBL, so reading all data as SGL is a poor choice, because it needs to be coerced later anyway, leading to extra memory allocations. Look at all these red dots!
• You can simply read your file using read delimited spreadsheet with space as delimiter. No need to jump through all these flaming hoops! (also building arrays in a shift register is the same as autoindexing at the output tunnel!)
• Your initial parameters are in the range of "almost -inf" to e^2, A more reasonable choice would be the natural log of an even distribution that sums to 1.
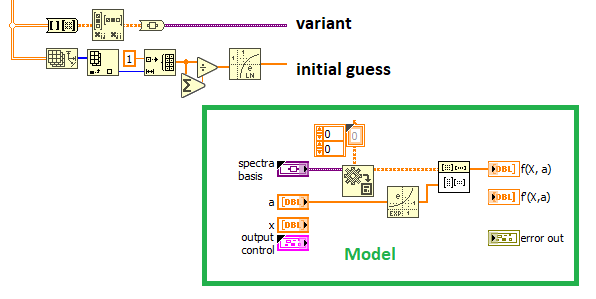
• You model is a simple Matrix x Vector multiplication, so create the matrix as variant and do the model as in the picture. No loop needed!

I'll attach my very fast code later. It's on a different computer.

[patriziocandeloro]

Dear Altenbach,

thanks a lot for your optimization of model as matrix vector multiplication and for the choice of initial parameters, they both look brilliant and elegant.

As soon as I will be at the computer I will implement them in the main software.

Unfortunately I saw the red dots of SGL to DBL precision conversion, I have to work on it because all the main software is using SGL precision. Maybe I should go back to DBL in all the code and all the subVIs.

I will get you updated as soon as I will use your model and initial parameters,

all the best,

pat

[altenbach]

The benefit of SGL is overrated unless you use massive datasets. You can easily read your files as DBL.

[altenbach]

OK, here's my fast code (LabVIEW 2016). See if it works for you...

For simplicity, it reads the file in a path relative to the VI. You can easily change that.

Solution takes about 300ns (compared to 100ms for your code), or about 300x faster.

(Not shown: I can do another doubling of the speed by some highly tuned explicit linear algebra, but let's keep it simple 😄 )

[patriziocandeloro]

Dear Altenbach,

thanks a lot for your code, it's truly fantastic and so fast. Considering that in several cases i have up to 150.000 curves to be automatically fitted, the high speed of your code is so helpful!!! And besides the high speed, the fitting results look perfect.

All the best,

pat