- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Sweep Sine Amplitude decreases
Solved!02-01-2015 12:19 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
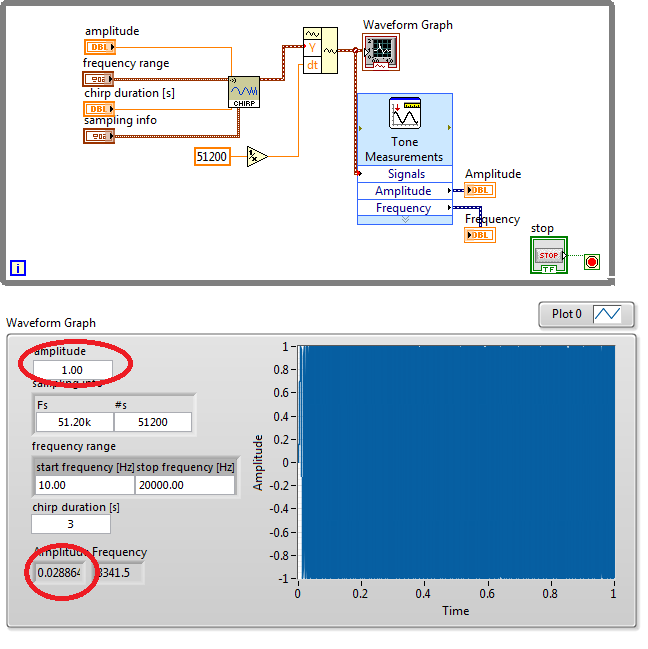
Hi All.
Why is the amplitude of my Sweep Sine decreases?
I wonder why increasing my number of samples, which is in my VI set to 51200 samples, results to an output amplitude of my sweep sine to decrease. However if my number of samples is small, let's say 1000 samples, the output amplitude from the Tone Measurements VI is close to one which is 0.968709.
How can I adjust in order to have the correct value of the amplitude. I need the amplitude to be exactly one, because I will output this in my DAQ.
Here is my VI.
Solved! Go to Solution.
02-01-2015 01:53 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Your sampling rate is ~2.5x your highest sweep frequency. While that meets the Nyquist requirement to find the frequency, you generally won't find the correct shape of a wave with such a minimal frequency. You want to be somewhere 10x the frequency or higher, if possible. Once you reach the 10x point, you get to a realm where you can start to consistently put the shape of the wave together.
02-01-2015 02:12 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Even if I set my Fs, sampling frequency to be 10x greater than my highest freq. When I increase the number of samples, the amplitude really decreases.
02-01-2015 10:17 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Try a ratio of 10:1 Fs:#samples.
That's usually about the sweet spot.
02-01-2015 10:39 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Obviously your chriped sine getting to 1,-1 - very close to those values of amplitude, your just not able to see it, try to see it with comparison that will light when the values of the amplitude are bigger , let's say than 0.999.
02-01-2015 08:27 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
The problem is I need to connect this chirp signal to a Play Waveform VI. If I have a ratio of 10:1 for the Fs:#samples, I'm getting a sound that is not continuous.
02-01-2015 08:56 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Although I agree with the sampling rate discussions above, you might consider normalizing the output of the Swept Sine to One? There is even a built in VI for it: "Normalize Waveform.vi"
02-02-2015 06:55 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
The use of Tone Measurements.vi is largely meaningless. Read the help for that VI. It finds the frequency where the amplitude is the largest. It uses Fourier transform techniques to find that frequency. The Fourier transform of a chirp ideally is a constant. Because the actual chirp does not cover an infinite frequency range and last for infinite time, the spectrum is modified by the effective window. Thus the peak of the spectrum is approximately at the center of the frequency range.
Drop a spectral measurement VI on the block diagram and plot the spectrum.
When I extract a subset of the chirp array and feed that to Tone Measurements I get much more reasonable values. Subset starting at sample index 15000 and having length 50 samples returns Frequency = 5876.21 and amplitude = 0.99999. The graph shows about 5 3/4 cycles in about 1 ms, which is consistent with the measured frequency.
Lynn