- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Plane surface plot with 3 points?
09-02-2010 07:37 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello everyone,
I'm trying to plot a plane on a 3-D graph based on three points. But the best I can get is a line connecting all three points. Is there any way to make a surface plot of the given data?
Also, the plot that I'm adding this to has a bigger coordinate range than the selected points. Is there any way to easily set the plane to extend to edges of plot?
I attached my code. Most of the program calculates the equation of the plane based on the three points, but I don't really use that here.
Would appreciate some advice!
Alex
09-03-2010 12:12 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
With the 3D surface plot, you have to enter a 2D matrix that defines the z values over every point in the xy plane. In order to do what you want you would have to interpolate what the rest of the values in the matrix would be based on the original 3 points. Definitely a possibly task, but not trivial. I spent 10 minutes trying to figure out the math for this, but I'm not too keen on geometry. However I know it can be done.
09-05-2010 07:35 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hmmmmm ok. That's the route I was going, which is why I calculated the determinants to ultimately figure out the equation of the plane. I can probably just run a bunch of points through the equation and get a dataset, but I was just wondering if I was doing more work than I needed to.
Thanks!
Alex
09-07-2010 01:07 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Nope, you were doing the right thing. If you end up creating an all-in-one VI that converts 3 points to a plane that can be plotted with the 3D picture controls, feel free to post it here or on ni.com/community as a community example. This way others in the future can use it if they have the same problem you are seeing.
07-16-2022 04:16 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I too am stuck with same issue.
07-16-2022
11:38 AM
- last edited on
07-18-2022
11:21 AM
by
![]() NI_Community_Su
NI_Community_Su
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
This sounds like a homework assignment but, the math is fairly simple if, you know how to do it.
You have 3 pts [D, E, F] with Cartesian coordinates known ( if you have rho, theta, phi convert to Cartesian its easier to imagine the spacial relationships and imagining those will teach you a lot!)
You also can define three lines from D-E, E-F & F-D each line will intersect at least one X, Y or Z plane and if it is parallel to one plane it must be normal to another else it will intesect all three planes.
So we can pick and chose points D and E {X Y Z} and {X Y Z}1 and do a little vector addition to get vector P and E an F {X Y Z}1and {X Y Z}2 get Vector Q and the cross product, P cross Q, defines the normal vector , "n"
Hold it, I just defined points D E and F as vectors with X, Y AND Z VALUES. A VECTOR is one element of a MATRIX you should be using the Matrix functions!
Now that we have the normal vector n, and not just 1 but 3 points known to be on the plane we can choose any one of those points to define the plane in 3D Space.
https://mathinsight.org/forming_planes
And we are certain n•(x—a)=0 for all points on that plane.
"Should be" isn't "Is" -Jay
07-17-2022 08:10 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@gokuravi wrote:
I too am stuck with same issue.
It is probably not useful to revive a 12+ year old thread that has already been answered. What exact issue are you having?
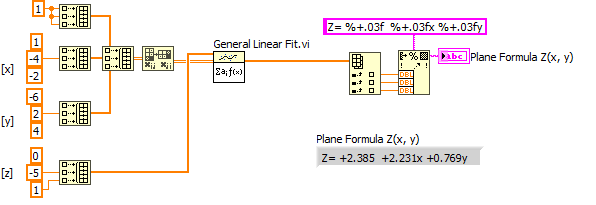
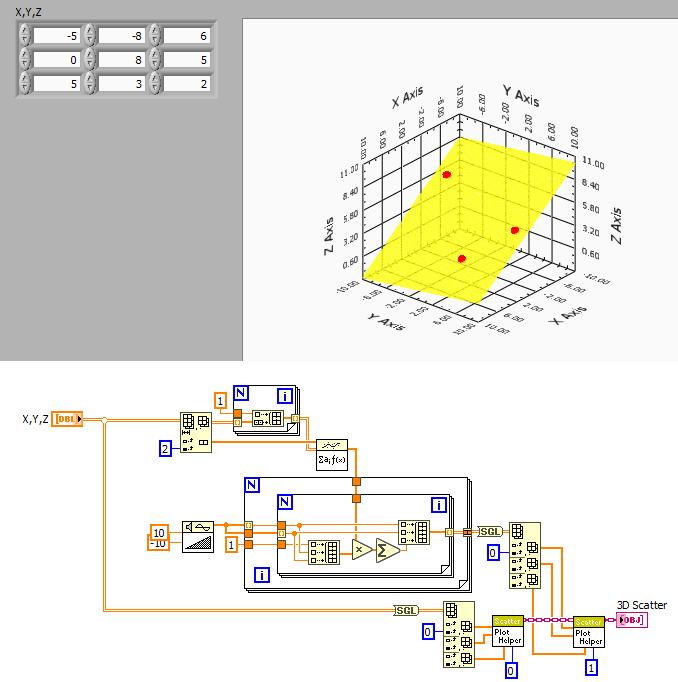
All you need is find the plane parameters, then calculate Z(xy) for point you desire, e.g. for a reasonable grid of your graph area. All this is is a simple 2D polynomial fit and you can use general linear fit for that.
This should get you started (using the values of the original old VI above).
07-17-2022 09:12 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator