How to write certain mathematical functions in the formula string of the downhill simplex nD i

[altenbach]

---

@altenbach wrote:
Long ago I have written a "drop-in" replacement for nonlinear curve fit that uses Nelder-Mead downhill simplex, where the VI model is defined as the same strictly typed subVI as used by nonlinear curve fit. Clearly this is something that NI needs to offer.

---

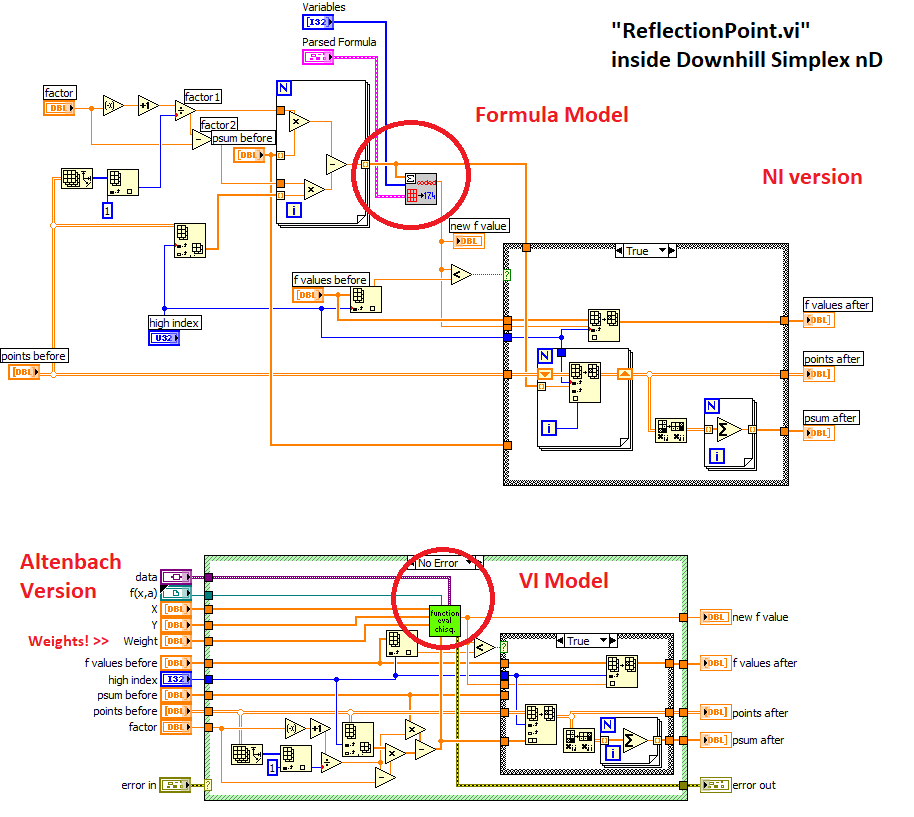
Most of my code was loosely based on the "Downhill simplex nD" from NI and it was relatively trivial to replace the formula parsing with a VI model. (I also added a "weights" option because LM has that).

For example, here is the "reflection point" subVI code. Except for the model calculation they are very similar, one just has a bit more lipstick and looks more polished 😄

[altenbach · Accepted solution]

OK, I removed some of my specializations and have posted a "VI model" version of my Nonlinear curve fit (Nelder-Mead). See if it can help with your problem. No guarantees 😄

[blessedk]

Thanks Altenbach. Yes my model should be easy to specify as a Vi (at least easier than any other option I guess)

I am expecting some experimental data next week so then I will be able to check things out, including your newly published Nelder Mead with vi Model input.

Like you said sometimes the derivative of f'(x,a) creates challenges. This may or may not be the case with me, but I will confirm. As it is now, It appears I have two possible approaches:

1. With your new Nelder mead vi, I can easily use the downhill simplex, which means that ultimately my function/model to be minimized would not be my Fmodelled, but instead a least squares function relating the Fmodelled and Fexperimental. That is Summation {(Fmodelled-Fexperimental)^2}.  (Guess am right?)

2. Alternatively (and if getting the derivative of my Fmodelled wont be an issue), then I will use the Non-Linear curve fit LM. which allows me to specify the experimental data points as (X,Y)

Question: What goes horribly wrong when f'(x,a) input is left floating?

You asked how else am I describing a discrete function. if am going for option 1 (Nelder mead), my intention is to evaluate fmodelled(x,a) at each xi corresponding to each discrete experimental point, get their difference, square and sum. The resulting model function will be only a function of "a" ie f(a1, a2....)

My Fmodelled will consist among other terms, an integral function and this integral function can only be treated as a discrete function of x (It is another dependent variable dependent on x, which has only experimental data (no formula relationship) so I will be evaluating that using definite numerical integration between x0 and xi where x0 is the first point and xi is subsequent points (x=1, 2, 3..) At x=3, the definite numerical integral will be evaluated between 0 and 3, and at x=4, between 0 and 4 and so on.

Which brings me to another question (not key to what I am doing now but good to add in). What makes the simpson's method better than the trapezoidal for example (if it is)?

[Bob_Schor]

---

@blessedk wrote:

Which brings me to another question (not key to what I am doing now but good to add in). What makes the simpson's method better than the trapezoidal for example (if it is)? 

---

A good question.  There is a Wikipedia article on Simpson's Rule which explains its relationship to the Trapezoidal Rule.  The Web is a good way to satisfy initial curiosity; a good course (or textbook) on Numerical Analysis will let you "learn at your own pace".

Bob Schor

[blessedk]

Yes you are right. But if sample very closely like we do I won't bother with a Simpson's and I can get less  non-NaN Values. Pros and cons 

[altenbach]

---

@blessedk wrote:

Which brings me to another question (not key to what I am doing now but good to add in). What makes the simpson's method better than the trapezoidal for example (if it is)?

---

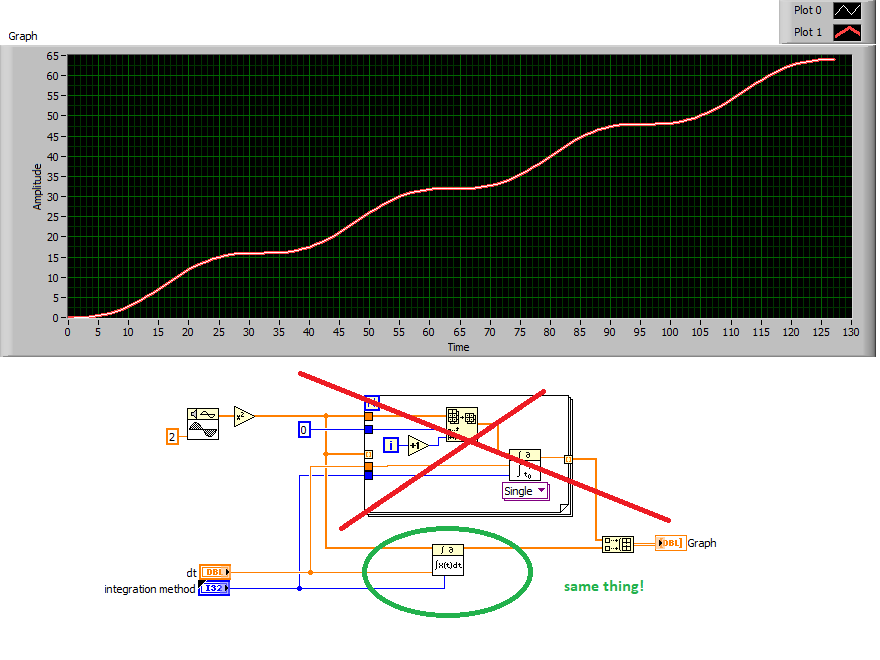
As a first step, get rid of that FOR loop where you are chopping up the array N ways. All you need is this function. same result. (see image).

I agree that these integration methods are pretty pointless for real data that has noise and is sampled at a higher rate than all critical features of the lineshape. I typically use trapezoidal. (In a pinch, you could just take the array sum and divide by dt. :D)