How to analyse this frequency response measured by labview?

[Lancelot3718]

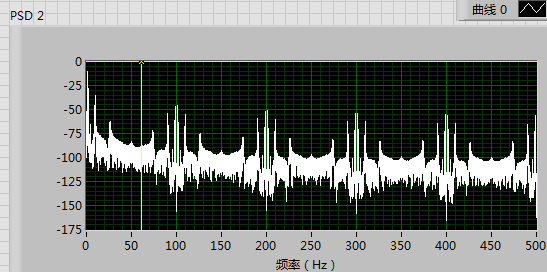
I use a 0—500Hz sweep sine signal to stimulate a cantilever and get a respone graph like this.

We can easily find the firts three modes in the left of the yellow cursor.But in relatively high frequency range, the magnitude-frequency characteristic saw a periodic change every 100Hz, while I think this is not reasonable. How can the magnitude of the higher modes bigger than lower modes? The periodic symmetry  of the magnitude is also hard to understand.

the vi I use to measure the response signals is this

How to explain this figure? Do all these magenitude peaks really stand for the modes of the cantilever?

[RavensFan]

They look like harmonics of the first 100 Hz resonant frequency.

But something is a little too odd about them.  They have very similar shapes, and there is a reflection at every 50 Hz point.

At what frequency was the sine wave sweep at when you took this FFT?

It looks like the FFT was set for power spectrum or dB on the Y axis.  Try looking at one for amplitude on the Y axis.

Show the time-based waveform as well.

[Bob_Schor]

I agree.  While my expertise is certainly not in mechanical engineering (so I don't really know about "modes of a cantilever"), the regularity and repetition of the response (with almost no decrease in magnitude!) at 100, 200, 300, 400, and 500 Hz looks very artifactual to me.  I, too, would like to see a waveform of the stimulus and a waveform of the response.  It might also be useful to see all of the relevant code (I recommend compressing the folder holding all of the VIs and attaching the resulting Zip file -- you might need to indicate to us which is the Top Level VI).

Bob Schor

[CoastalMaineBird]

Looks like aliasing to me.

What is your DRIVE signal and waveform?  If you're driving at 500 Hz (sinusoid), you need to be sampling at 1000 Hz minimum.  It looks like you might b sampling at 200 Hz, and you get aliases.

If you drive at 500 Hz with something other than sinusoid, you have to sample higher than 2 x or, use filters.

[CoastalMaineBird]

Looks like aliasing to me.

What is your DRIVE signal and waveform?  If you're driving at 500 Hz (sinusoid), you need to be sampling at 1000 Hz minimum.  It looks like you might b sampling at 200 Hz, and you get aliases.

If you drive at 500 Hz with something other than sinusoid, you have to sample higher than 2 x or, use filters.

[Bob_Schor]

Duh -- good point about aliasing -- I should have thought of that!  Duh -- good point about aliasing -- I should have thought of that!

Bob Schor

[Lancelot3718]

Hi，RavensFan:

Thanks for your help.

The ferquency range of  sweeping sine wave is from 0 to 500Hz.

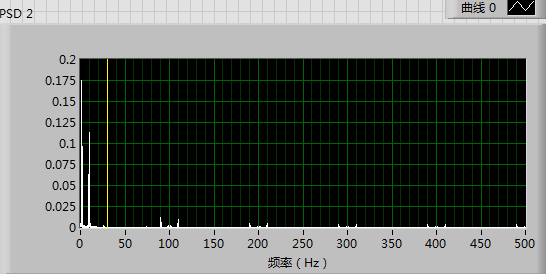
No, the FFT was a for the magenitude (peak value), and the unit of  Y aixs is dB.

This is the absolute amplitude graph:

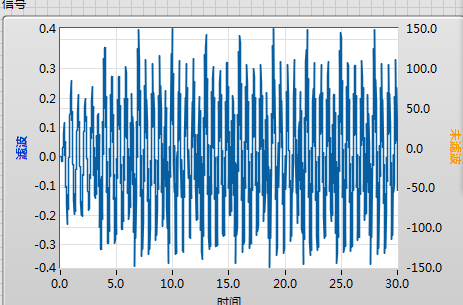
The time-based waveform is this：

Thank you again~

[RavensFan]

I had always thought of aliasing as causing a single reflection back across the FFT.  I've never seen a situation of multiple reflections that are repeating each other.  I'd love to see the original waveform, along with all the settings that were used to acquire it.

[RavensFan]

---

@Lancelot3718 wrote:

The time-based waveform is this：

---

What are the units for the X-axis?  Is that 30 seconds, 30 milliseconds, 30 microseconds?

What is the acquisition rate of that signal?

What was the specific frequency of generator during that period of time shown on the chart?

[Lancelot3718]

Hi Coastal：

Thanks for your help

The drive signal is a sweep sine signal （0—500Hz)

Yes, my sample frequence is 1000Hz, not 200Hz, but I do not know how to set this vi's sample frequence, what I can do is to set the time base signal's  'dt ' as 0.001s, like the picture below:

In fact, when I use a sweep sine signal (0—50Hz），and the output is still the same (sample frequence is still 1000Hz), like this:

So, I do not think this is aliasing.

Here is my vi , maybe it cannot work on your PC, it may still help, please check.