LabVIEW
Efficiency of Cartesian to Spherical coordinate conversion
Solved!
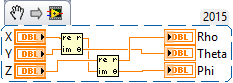
Use simple complex math. Seems to work and gives the same result as "cartesian to spherical".
Please test and see if it is correct.
(Works equally well with SGL, DBL and arrays of any dimension.)
Definitions are extremely important in defining coordinate systems. The documents that you include with your Cart_to_Sph VI contain numerous mistakes and inconsistencies.
Here is a convention that I use and that seems to have a reasonably wide acceptance (I'm not sure that this is the Wolfram convention, however).
Let X, Y, and Z be a right-hand coordinate system. Let P be a point whose X, Y, Z coordinates we know. Define a Spherical Polar Coordinate (SPC) system as follows:
- Project a line from the Origin to P.
- Radius (rho) -- Length of the line from the Origin to P.
- Project the line onto the X-Y Plane.
- Azimuth (theta) -- Angle measured counterclockwise from the X axis to this Projected Line. By convention, theta ranges from minus pi (radians) to pi.
- Polar angle (phi) -- the angle between the Z Axis (or "pole") and the line from the Origin to P. By convention, phi ranges from 0 to pi.
Under this coordinate system, the following code (very similar to Altenbach's, which uses a slightly different coordinate system) maps X, Y, Z into Rho, Theta, Phi:
Let's check some "known quantities". Start with the Unit X axis, [1, 0, 0]. This clearly has length, Rho = 1. The X axis lies in the XY plane, so the angle between it and the Z axis is 90°, so Phi should be pi/2. Finally, the projection of the X axis in the XY plane lies along the X axis, so the angle between the two X axes is 0, so Theta should be 0. The first Re/Im to Polar will give 1, 0, so Theta = 0. The second will give 1, pi/2, so Rho = 1 and Phi = pi/2.
How about Unit Z, [0, 0, 1]? Again, the length, Rho, is 1. Technically, since the Z axis projects onto the origin, the azimuthal angle cannot be properly defined (as both X and Y coordinates are 0), so we'll do a "math cop-out" and just say it's zero. The Polar angle is easy -- the angle between the Z axis and the pole, the Z axis, is 0, so Phi = 0. Now "do the math". Putting [0, 0] into the first Re/Im to Polar gives [0, 0], so Theta = 0. The second Re/Im to Polar takes [1, 0] into [1, 0], so Rho = 1 and Phi = 0.
It is easy to show (especially by coding this up and putting in test numbers) that negative quantities work properly. Rho is always non-negative, Phi is always in the range 0 .. pi, and Theta is always -pi .. pi, with the sign dependent on the sign of Y (as it should be).
Bob "Just Do the Math" Schor
P.S. -- if you think this is fun, just try 3-D rotation matrices ...
Yes, all I did was to ensure that it gives the same result as 3D Coordinate Conversion VI in the way it was wired. There are many ways to define the system...
@Darin.K wrote:Use atan2(y,x) instead
Of course "atan2" and "RE/IM to Polar" give you the identical result for the angle, but with the complex primitive we also get r for free, which we need here anyway.
Some quick benchmarking shows that the complex version is only a few % slower* (but it also caclulates r!). If we use atan2 and calculate r seperately, we are slower than the complex version.
Complex also wastes less diagram space. 😄
* note that these speed differences are irrelevant and many other code changes have similar subtle effects. Unless we get at least a factor of two, I don't worry and go with the cleaner code. 🙂
