Backward Euler Integration

[CamW]

Hello everyone,

I am writing a VI to simulate the response of a hydraulic system. Most of the program runs perfectly, but certain sections require integration which has proved to be a problem.

I have attempted to use 'Numeric Integration.vi', and have written a forward Euler subVI, which both fail to converge due to the nature of hydraulic systems. It seems that Backward Euler integration is the solution, but I have been unable to find a way to implement it.

I have tried evaluating the 'Control Design and Simulation' module, which has a range of integration methods, but the module itself seems unsuitable.

I was hoping somebody would have a better understanding of the equations than me, as the implicit nature of Backward Euler is causing me some difficulty.

Edit: I have attached a snippet which I have been using to test out possible solutions. It provides testing data and compares the result to the value I am aiming for, which was generated using different software.

Thanks,

Cameron

[CamW]

If anyone gets an opportunity to try out this code, the iteration value should be connected to subset length, not subset index.

[altenbach]

Just a side note: Your upper code can be replaced by a simple integral x(t).vi. Same result.

[ToeCutter]

No dice with existing methods if you decrease your simulation timestep?

[CamW]

Thanks altenbach, I'll put that into my testing version.

Unfortunately not ToeCutter, I've reduced it to the lowest value I can and it still diverges after less than a second.

I've tried running simulations on some other software (which has various built in integrators) and Backward Euler seems to be the only method I can use.

[Supreeth.K · Accepted solution]

Hi CamW,

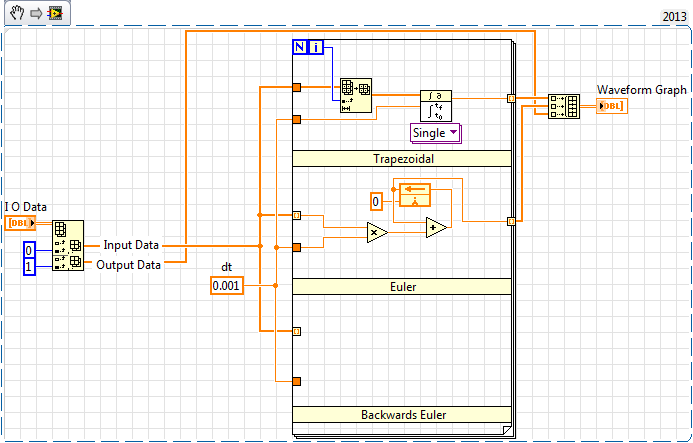
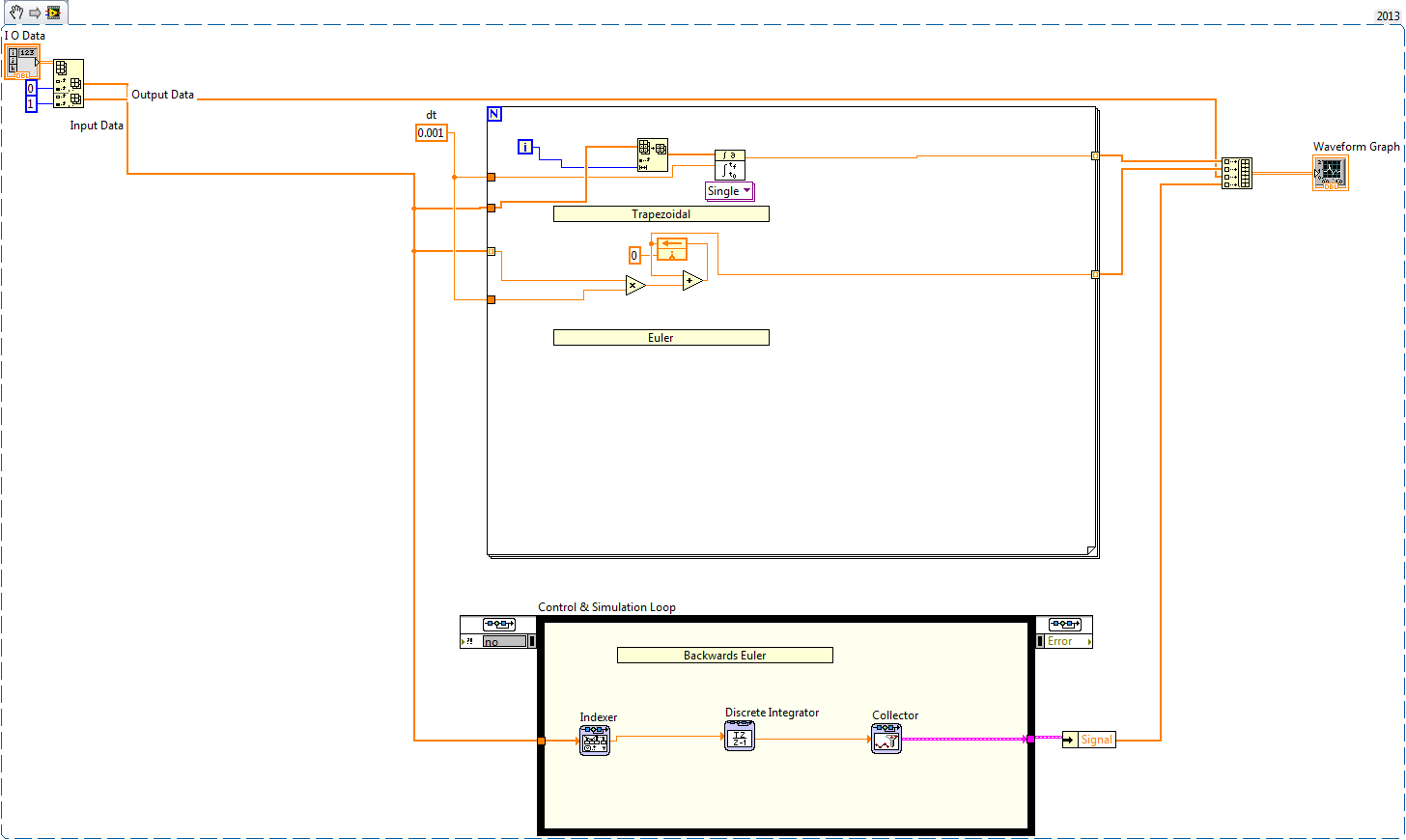
You can do the backward euler integration in labview by using the Discrete integrator funtion from the control design and simulation module as shown below:

Thanks and Regards,