All possible permutations (with repetition) of a 1D array given a new array size

[adamchick]

Hello,

I am trying to come up with an algorithm which generates a 2D array (size n^k, k) of all possible permutations (with repetition) given a 1D array (size n) and available slots (k).  The 1D input array will contain a set of unique elements (i.e. no duplicates).  Here is more detail:

Inputs (as an example):

1D array:  [1 2 3 4 5]

Available slots:  3

*** Therefore, n = 5; k = 3 ***

The algorithm would output a 2D array (size 5^3, 3):

[1 1 1

1 1 2

1 1 3

1 1 4

1 1 5 ...

5 5 3

5 5 4

5 5 5]

I've achieved this using nested for loops (number of for loops equal to k) (shown below), but this solution is clunky, not easily scalable, slow, etc.

This part of a larger program where each permutation will be evaluated.  Note that order matters; for example, [1 1 2] is different than [2 1 1] and both must be present in the 2D array.

I'm using Labview 2016.  Thanks for your help!

[aputman]

This sounds like an Algorithm Analysis college class homework assignment? 

[adamchick]

I suppose it could be, but that's not my application.  

I'm iterating through multiple spring constants - the 1D array represents a specific family of springs - and am trying to use Labview to quickly generate all possible permutations of these values.  

My brute force method (nested for loops) is working fine; just wanted to reach out to see if someone had input on a more elegant (and efficient) way of doing this.

[Minions]

Aren't Permutations with repetition called Combinations? nCk

[aputman]

I suspect this will involve some recursion, but I would also think it can be solved without.  And since I don't want to try to figure it out, I'll post some links.

[Mancho00]

using recursion..

... and yes there may be a few stray wires...

[altenbach]

This is slightly different to this old problem, but the way I see it, all you need is counting up to the largest possible three digit number in a Quinary system, easy to do using quotient &remainder.

Shouldn't take more that a postage stamp worth of code. 😄

[altenbach · Accepted solution]

---

@altenbach wrote:

Shouldn't take more that a postage stamp worth of code. 😄

---

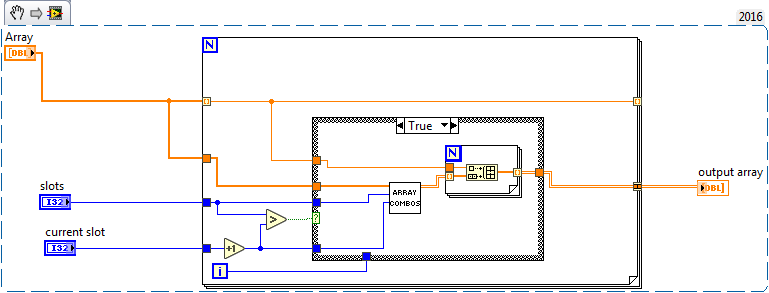
Here's a quick draft. Modify as needed.

Also note that it works for any size input array and number of digits (within reason, of course! ;))

(... and yes, it took me much less time than the 14 minutes since the previous post :D)

  

(Note that the first loop is just a "blue" exponentiation)

[Kevin_Price]

The recursive solution from Mancho00 is much more elegant than the messy iterative one I was working up, and therefore won't bother posting.  

Recursion is efficient in terms of the quantity of source code to be maintained.  Your nested For Loop solution is probably pretty efficient for execution time (likely noticeably faster than recursion for large 1D arrays & large #'s of slots).

The main downside I noted in your screenshot was the need to hardcode #'s of nested loops in distinct cases and then feed a hardcoded # of branched copies of the 1D array into those loops where only some of them usually get used.  The recursive solution makes those things unnecessary.

All I did below was to turn Mancho00's snippet into an actual vi so I could set it up with reentrant execution properties and to make it more clear that the visible "outer" code is literally the internal contents of the "inner subvi" being called.

-Kevin P

P.S.  Too late, altenbach posted a better solution between the time I started and when I got around to finishing...

[aputman]

I knew Altenbach would be around shortly to figure this one out.  Right up his alley of "doing more with less code".