CVI Cubic spline for scattered points

[erickringot]

Description

Description-Separate-1

Interest of cubic splines

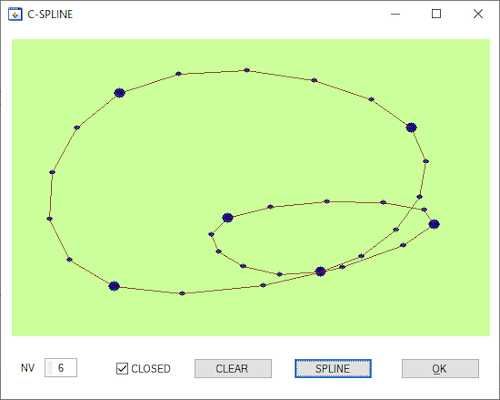
After having sampled data, in order to represent them, it can be useful to join the corresponding dots by a smooth curve rather than an ordinary series of straight segments. This article deals with cubic splines (c-splines) for such a purpose. The dots, in two dimensions, can be scattered on the plane in any order or location. Therefore the x-coordinate doesn't need to be in ascending order, as the Advanced Analysis Library  'CubicSplineFit()' requires, such enabling the curve to intercept itself, to form loops or even to be closed. The function provided at the end of this article is much easy to use than 'Spline()' as well ; there is no need to give the derivatives or second derivatives "by hand". Only the location of the primary points is required.

A bit of theory

Source of information

modGEOM_fr Ricardo CAMARERO
Département de génie mécanique, École Polytechnique de Montréal, Janvier 2019
https://moodle.polymtl.ca/pluginfile.php/16154/mod_resource/content/6/modGEOM_fr.pdf

-in easy and clear French-

Chap. 3, pages 19-31

Short principle explanation

Let be n points (2D-vectors) A0, A1 ... Ai ... An-1

The goal of this article is to show how to build a continuous, smooth (derivable) curve going through these points. The curve is chosen as a series of cubic sections joined together.

We introduce the derivatives: D0, D1, ... Di ... Dn-1 (2 coordinates) and the curvatures: C0, C1, ... Ci ... Cn-1, at the location of the points Ai.

According to the cubic spline method, therefore based onto the mathematical C0/C1/C2 continuities at each point Ai inside the curve, the interpolation of any point on the desired section delimited by Ai and Ai+1 is got by:

P(t) = H1(t).Ai + H2(t).Ai+1 + H3(t).Di + H4(t).Di+1  with t in [0,1]

Hk being a Hermite polynomial among:

    H1(t) = 2t^3 - 3t^2 + 1
    H2(t) = -2t^3 + 3t^2
    H3(t) = t^3 - 2u^2 + t
    H4(t) = t^3 - t^2

Actually, Di (and Ci) are unknown; the only known information is the point locations the cubic spline curve must go through.
The calculation method consists in evaluating the derivatives which are solution of the following linear equations [H].[D]=[S].

• [H] is a square matrix
• [D] is the vector of the derivatives (2 coordinates each)
• [S] is a known second member based onto the locations [A]

Two cases have to be considered:

--- 1 --- case of the opened spline (condition of curvature null at the boundaries).

|2 1          |   |D0  |     |A1-A0      |
|1 4 1        |   |D1  |     |A2-A0      |
|  1 4 1      |   |D2  |     |A3-A1      |
|     .....   | . |... | = 3.|....       |
|       1 4 1 |   |Dn-2|     |An-1 - An-3|
|         1 2 |   |Dn-1|     |An-1 - An-2|

--- 2 --- case of the closed spline

|4 1        1 |   |D0  |     |A1 - An-1  |
|1 4 1        |   |D1  |     |A2 - A0    |
|  1 4 1      |   |D2  |     |A3 - A1    |
|     .....   | . |... | = 3.|...        |
|       1 4 1 |   |Dn-2|     |An-1 - An-3|
|1        1 4 |   |Dn-1|     |A0   - An-2|

[H] is always positive and symmetric, making the system inversion simple and fast.

C language Code

All the steps of calculation are contained in a single function 'Cspline()' heavily commented and available in the attached C source.

Description-Separate-2

How to Use

How-Separate-1

The project 'spline' can be used a stand alone example, for that, under Labwindows/CVI you must choose the option EXECUTABLE as the target type. The generated program exhibits an UIR with a canvas on which the user can define a series of points, choose if the curve must be closed or not and launch the plotting of the spline.

In case the target type is defined as 'STATIC LIBRARY', the file 'spline.lib' can be used in another program provided the following declaration is made:

extern void Cspline(int panel, int control, int cflag, int np, Point P[]);

• cflag = 0 (opened) or 1 (closed spline)
• np = vertice number
• P = array of vertices

Don't omit to properly set the drawing parameters of the canvas:

• ATTR_PEN_COLOR
• ATTR_PEN_MODE
• ATTR_PEN_WIDTH
• ATTR_PEN_STYLE

How-Separate-2

Additional Information

Additional-Separate-1

Labwindows/CVI 2017

Use the Advanced Analysis Library for the matrix inversion (function SolveEqs) but a Koleski method could be fine as well.

The number of interpolating points is given by the constant N (currently 5).

Additional-Separate-2