Curriculum and Labs for Engineering Education

edoering · ‎07-13-2010

Course Linkage: Linear Circuit Analysis >> Resistive Circuits >> Series Resistors

Measurement Techniques: ELVISmx DMM (ohmmeter)

<hr width=”75%”>

Introduction

Overview: Two-terminal devices connected together in series share a common current. Resistors connected in series behave as a single equivalent resistance whose value is the sum of the individual resistor values.

Objectives: In this mini-lab you will:

Learn about resistor color codes
Measure the resistance of individual resistors
Compare measured resistance to nominal value
Predict the equivalent resistance of series-connected resistors
Compare measured equivalent resistance to expected values

Equipment

NI myDAQ
Breadboard
Connecting wire
Resistors, ¼-W 5% carbon film: 10K (two), 33K (two), 47K (two)

Deliverables

Submit your work in the form of a homework set problem or lab notebook entry according to the requirements of your instructor
Submit your work for each underlined boldface item, and clearly label the item with its section letter and task number

A. Experience series-connected resistors by measurement

Study the short article Resistor Color Codes to learn how to read the nominal value encoded in the color bands that encircle a resistor. For example, the 10K resistor has the color code “orange-orange-orange” = 33 x 10^3 = 33 kohm.
Record the color bands for the 10K and 47K resistors.
Place the six resistors on your breadboard as shown in Figure 1. Use the same hole spacing to match the wiring that will be added later.
Start the ELVISmx Instrument Launcher and click "DMM." Choose the ohmmeter instrument (the “ohm” symbol, capital omega), select autoranging (choose “Auto” for “Mode”) and click the green “Run” button:
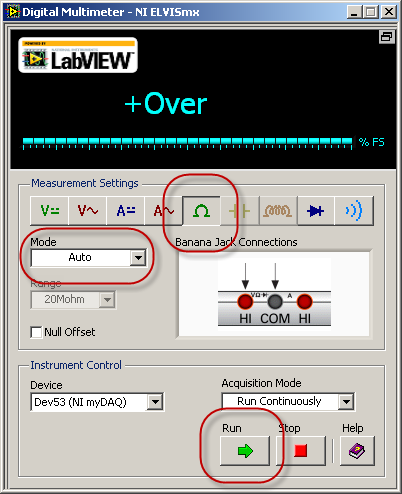
Connect the DMM probes to the ohmmeter side (red volt-ohm and black COM jacks) as shown on the ELVISmx DMM “Banana Jack Connections” graphic.
Touch the DMM probe tips together to ensure that the ohmmeter properly reads zero or at most a fraction of an ohm. The probe cables have negligible resistance compared to the resistors used in this mini-lab.
Measure and record the resistance of each of the resistors R1 through R6.
Create a data table with four columns: resistor label, nominal value (i.e., the value indicated by the color code), measured value, and percentage difference from nominal. Calculate the last column as ((Rmeasured – Rnominal)/Rnominal) x 100%.
Report the largest percentage difference and whether or not it falls within 5% of the nominal value; this is the significance of the gold 5% tolerance band on the resistor.
Connect the resistors as shown in Figure 2:
Measure and record the combined resistance of R2 and R3; touch the DMM probe tips to the left and right extremes of the resistor combination.
Measure and record the combined resistance of R4, R5, and R6.
Respond: What do you observe about the equivalent resistance as an increasing number of resistors connect in series?

See the following video for some expected results for this section:

B. Learn the underlying principles

Two-terminal elements such as resistors connected in “series” share a common current. Connecting resistors together in series increases the effective resistance of the entire chain of resistors; the chain may be viewed as a single equivalent resistor whose value is the sum of the individual resistances. The following video tutorial discusses series-connected resistors and derives the equation for the equivalent resistance of series-connected resistors:

C. Connect the principles to your measurements:

Rewire your breadboard to match the circuit shown in Figure 3:
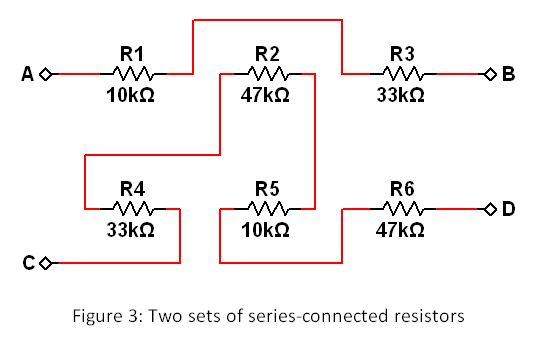
Draw a sketch of your new breadboard layout.
Calculate the equivalent resistance between terminals A and B using the nominal resistor values. Repeat this calculation using your measured resistance values.
Calculate the equivalent resistance between terminals C and D using the nominal resistor values. Repeat this calculation using your measured resistance values.
Measure and record the resistance between terminals A and B. Repeat for terminals C and D.
Calculate the percentage difference between your measured values and your calculated values derived from the nominal resistor values.
Calculate the percentage difference between your measured values and your calculated values derived from the measured resistor values.

D. Build your intuition:

Respond: What is the typical level of agreement between your measured equivalent resistance (say, terminals A to B) and your calculated equivalent resistance based on nominal resistor values?
Respond: What is the typical level of agreement between your measured equivalent resistance and your calculated equivalent resistance based on measured resistor values?
Respond: Is it possible for the equivalent resistance of series-connected resistors to be lower than the smallest-valued resistor in the chain? Explain your answer.
Respond: Suppose you have an arbitrary number (say N) of equal-valued resistors with value R. What is the equivalent resistance of these N resistors when connected in series?
Respond: Does the position of the resistor within the series-connected chain make a difference in the equivalent resistance? Explain your answer. If in doubt, try swapping the positions of any two resistors, repeat your A-B (or C-D) resistance measurement, and compare to your original measurement.