- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Curve fitting of two equations to one curve
10-23-2006 07:08 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
10-24-2006 02:26 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
10-24-2006 06:59 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
10-24-2006 07:04 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
10-24-2006 07:11 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
10-25-2006 01:19 AM - edited 10-25-2006 01:19 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
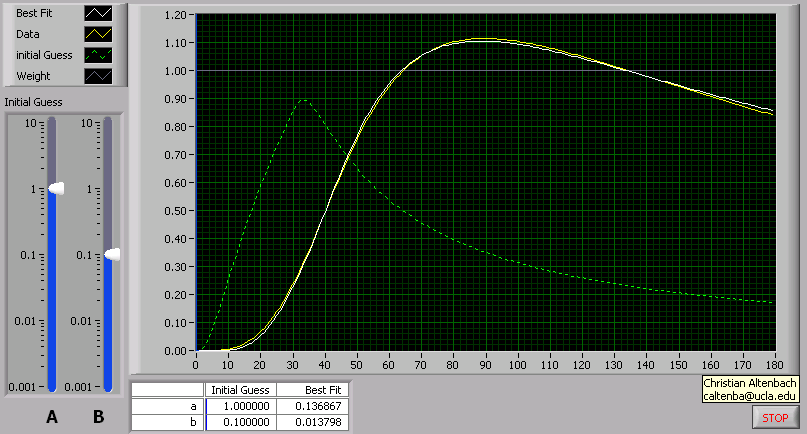
y=(1/a) * {Ei(1/(bx)) - Ei((1/b)/(x-30))}, for x>30
Message Edited by altenbach on 10-24-2006 11:22 PM
10-27-2006 12:25 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
10-27-2006 12:25 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
10-27-2006 03:20 AM - edited 10-27-2006 03:20 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
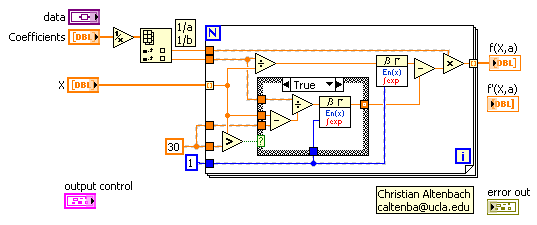
- Call the model function by reference so the fitting VI's don't need to be rewritten for each model.
- Make the model function work on arrays of x instead of one x at a time. This allows much more flexibility for the model.
As I mentioned, the LabVIEW 8.0+ fitting routines implement the above, and much more. If you get a change to upgrade, do it. 😉
Attached is a quick modification where I downconverted the 8.20 version mentioned in an earlier post to 7.1 and patched in my old fitting routines. They seem to work OK.
See how far you get and let me know if you have any questions. 🙂
Message Edited by altenbach on 10-27-2006 01:21 AM
10-27-2006 04:28 PM - edited 10-27-2006 04:28 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
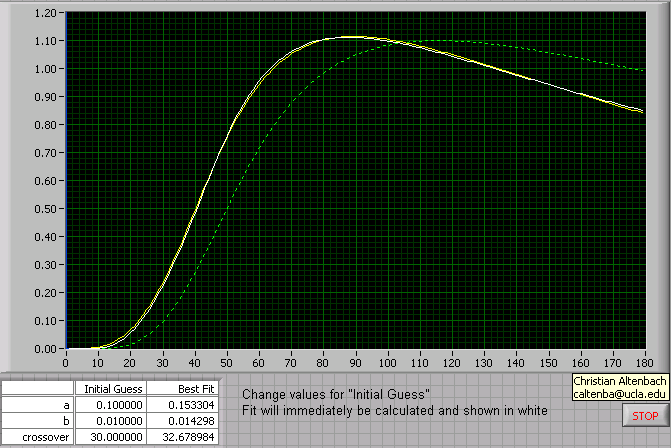
Message Edited by altenbach on 10-27-2006 02:28 PM