- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Nyquist theorem - Determination of Sampling Rate - FFT
04-29-2016 09:42 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Part of the issue is your terminology. The "frequency" does NOT drop to zero at 2 kHz. The amplitude of the frequency components just above 2 kHz drop to nearly zero. As Bob Schor pointed out your signal appears to contain significant energy to beyond 15 kHz. There appears to be a small component just below 30 kHz that may be the second harmonic of the 15 kHz signal.
It is also difficult to determine from a linear y-axis scale. The largest visible signal is just above 0.5. The smallest components seem to be about 0.1. If the data is sampled at 16-bit resolution with a full scale range of 1, then the smallest signal possible in the data is ~15E-6. By judging the content of the signal from the linear graph, you are ignoring 12 or 13 of the 16 bits.
Based on what I see, 100 kHz sampling is probably the slowest rate you should be using. If you know that all the interesting stuff in your signals happens at low frequencies, you will need a hardware anti-aliasing filter before the DAQ device to allow the use of lower sampling frequencies.
Lynn
05-01-2016 08:50 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
The data are sampled using 24-bit card with a full scale range of 1 and 100,000 Hz sampling is the highest rate the card can go up to. This signal is measured using a load cell with 50 Hz electrical noise without any load on it.
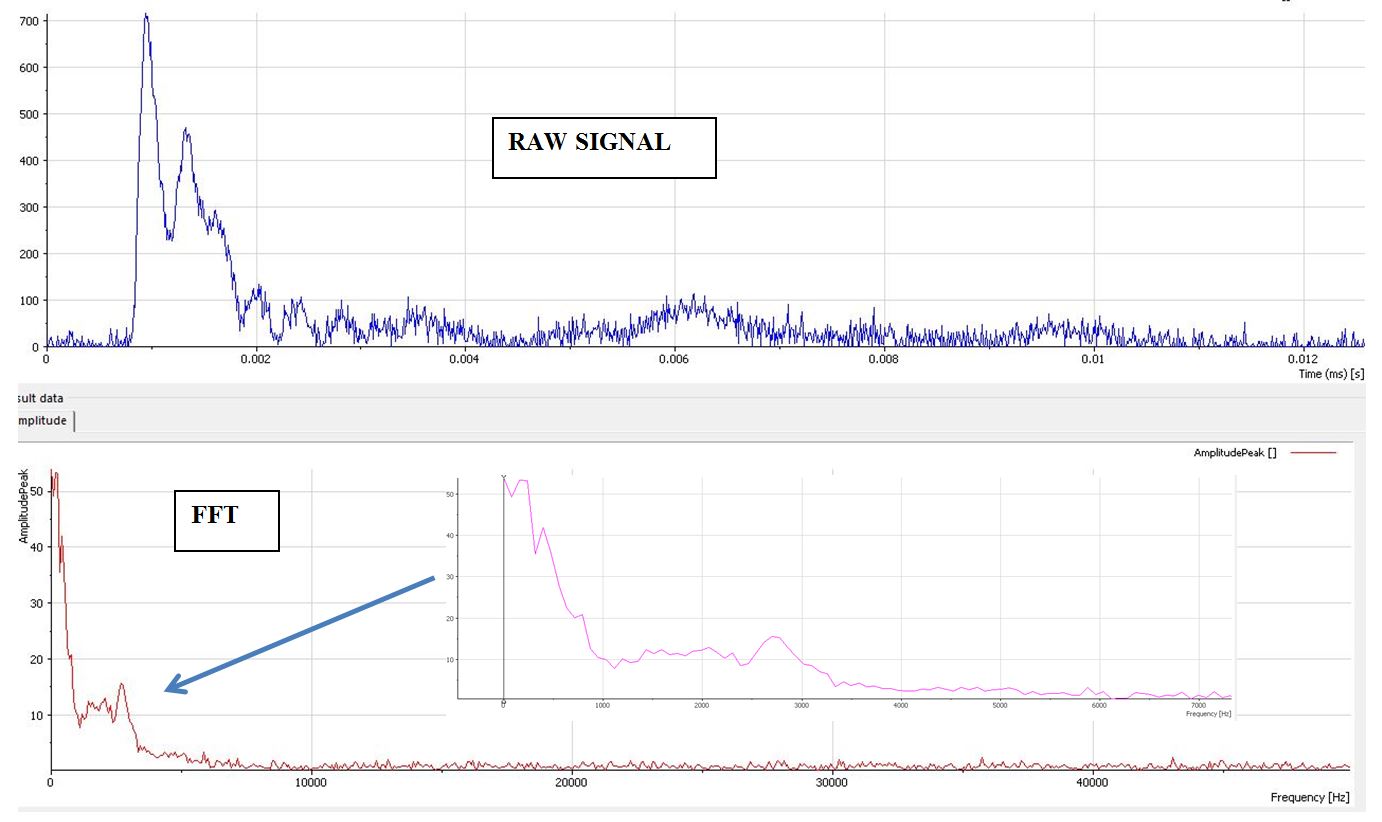
To bring some more light, I have done one more test with 100,000 Hz sampling frequency as shown below. Forget the previous signal. As JohnSold says, the amplitude of the frequency components at roughly 10,000 Hz drop to nearly zero and the signal loses its energy at around 10,000 Hz.
05-01-2016 10:35 AM - edited 05-01-2016 10:37 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@BradOconnor31 wrote:There are oscillations below 10 kHz and a peak at 15 kHz, but the frequency seems to stabilise after 15 kHz, despite the fact that there is too much noise in the FFT.
The intention is to use a low pass filter (Butterworth) to filter the high frequencies of the signal and also to correct the phase in the initial aplitude-time graph.
If I use sampling frequency 100 kHz , then the Nyquist is 50 kHz, I agree with that. But I want to use different sampling rates to establish which sampling shall I use, this is where I am confused. Also, what shall I use to filter the signal without eliminating the peaks or the majority of the signal?
Remember the assumptions of doing Fourier analysis, possibly the most important being that you are looking at a periodic signal, whose period is your entire sampling time. You don't have "too much noise in your FFT", you have too much noise in your signal. One thing you should always do before acquiring data digitally is to low pass filter your signal, often around your Nyquist frequency. You could also use various averaging techniques when sampling (this amounts to sampling over a longer time, getting more samples and averaging either before or after doing your FFT).
Do you know about Aliasing? If you sample at 100 KHz and have a Nyquist frequency of 50 KHz, any power in your signal above 50 KHz will appear and contribute to your spectrum at a lower "alias" frequency -- this is the reason you need to filter your signal before sampling it.
A "rule of thumb" that my engineering friends tell me is to sample an order of magnitude higher than the highest frequency of interest. So if your signal really does have interesting power at 15KHz, sampling at 100KHz makes sense. Filter, Sample, then Digitally Filter (note that averaging the spectrum is a form of low pass filtering).
Bob Schor
P.S. -- oops, I didn't see the subsequent posts, but I think my comments still hold.
05-01-2016 11:56 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thank you for the additional information.
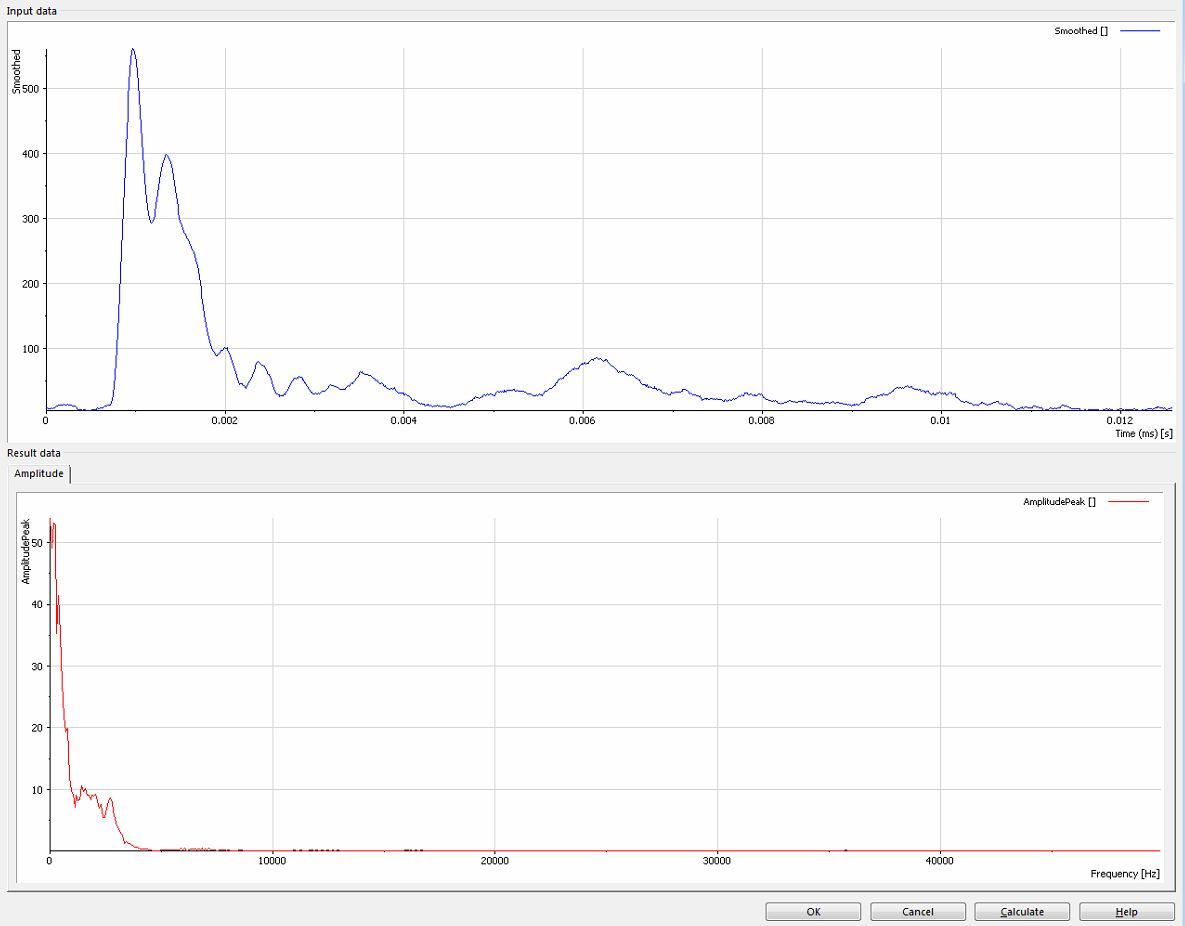
- Because your signal is generated by a load cell which appears to always be in compression (or tension, but not both), the signal has an offset. This results in the FFT having a fairly large zero-frequency component. Since the raw signal starts and ends near zero, my guess is that you do not care about the very low frequency components. If this is true, then subtact the mean of the data set before doing the FFT.
- The raw signal looks like an impact with a bounce and some ringing. Unless you suspect that the impact is exciting some resonance in the mechanical system, a frequency domain analysis may not be the best choice. What information are your trying to obtain from these tests?
- The 50 Hz component is not obvious in the raw signal and is hidden among all the other low frequency components in the FFT. It is almost always better to find and eliminate the source of power line interference before it gets into the digital data. This may involve eliminating ground loops, use of differential amplifiers, shielding, and isolation. Without more details about your system I cannot be more specific. Because 50 Hz appears to be within the frequency range of the signal you want to measure, the most appropriate method of reducing it may be very dependent on how your system is configured. Filtering after digitizing is almost always the last choice.
- What is the resonant frequency of the load cell? This could contibute to the 15 kHz peak in the first graph you posted.
- What is generating the forces to be measured by the load cell? What will you do with the data after you measure and analyze it?
Lynn
05-01-2016 06:37 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thank you both for your feedback. I am trying to achieve two objectives:
- Try to test the same steel beam specimen under impact load (two load cells and a steel beam spanning across the top of load cells) with the sampling rate as the only variable. More clearly, I am trying to convince the reader that 100 kHz sampling rate is adequate to capture the data from the load cells. Please ignore the first image that I posted on this with the 15 kHz signal frequency.
- Try to explain the FFT of the signal, check the frequency of the sample and find an appropriate filter to filter the frequencies. I am intended to use a low pass filter to: a) avoid the phase shift of the signal and b) not alter the peaks.
- The load cell measures only compression load (the compressive force interaction between the bullet and the sample). In my Vis, I used the single tone extraction vi. to check the frequency component of the load cell (rest position) which is 50 Hz because of the electrical noise or cabling. The load cell is connected with a hardware module and then to a PXI system where is controlled using labview.
- The raw signal is recorded from an impact test. Indeed, the signal has an initial peak at the time of contact and some ringing. I have applied a moving average and offset to the signal (post-processing analysis) as Lynn suggested, but there is again a large zero-frequency component as shown below.
Lynn - The load cell is the following: http://www.novatechloadcells.co.uk/ds/f218.htm
K = stiffness = 1.7 x 10^9 N/m
m = mass. The certificate gives the weight which is 1 kg.
The resonance of the load cell is fN = (1/(2pi)) * sqrt((K/m)) = 6562.13 Hz
- Bob-Instead of adding a low pass signal before the analog signal goes to ADC converter for digitization, can’t I just apply a moving average in the post-processing analysis?
- Aliasing & Nyquist
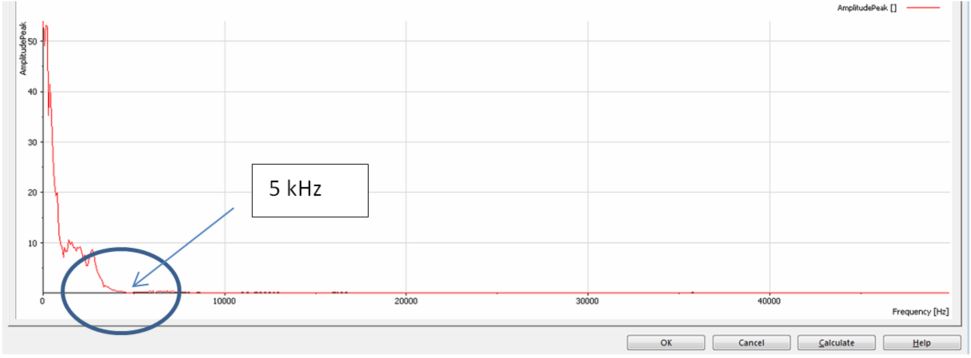
Please correct me if my thinking is wrong. If the analog signal (load cell) is sampled at 100 kHz, the Nyquist frequency is 50 kHz. Until now, ok. If we take the signal from the time domain to the FFT domain, the amplitude frequency becomes approximately 0 at 5 kHz as shown below. If the Nyquist says to sample two times the highest frequency of interest, isn’t it 5 x 2 = 10 kHz? So, we are 40 kHz safe?
05-01-2016 07:06 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@BradOconnor31 wrote:
- Bob-Instead of adding a low pass signal before the analog signal goes to ADC converter for digitization, can’t I just apply a moving average in the post-processing analysis?
Absolutely not! The purpose of low-pass filtering your input is to prevent aliasing. Suppose, through some fluke, a significant 90KHz noise signal gets into your system. When sampled at 100KHz, this noise will appear in your spectrum at 10KHz, not at 90KHz. Remember that 15KHz funny-looking peak in an earlier plot? Maybe it's 85KHz "noise".
Bob Schor
05-01-2016 07:21 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I understood your point , yes. Thanks.
05-01-2016 07:21 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Please post some of your raw data. Either post a VI with the data saved as default on an indicator or a file with the data saved as text or TDMS. I would like to look at the data and see what I can figure out.
I think you still have some misconceptions about sampled data systems. The Nyquist rate required to sample fast enough to reproduce the input exactly is based on ALL the energy in the signal including noise and interference.
Using the RAW SIGNAL and FFT images from a few posts back as an example, it appears that the noise at 50 kHz is about 2% of the highest component on the graph. This means that there is still a significant amount of moise energy in the input signal at those frequencies. When I expand the image and look at the data closely, it appears that there is a noticeable change from one sample to the next. The amplitudes appear to be on the order of 1% of the peak (impact) signal. If the random noise is that large, it is almost certain that you are getting some noise aliased into your data. THERE IS NO THEORETICAL OR PRACTICAL WAY TO REMOVE AN ALIASED COMPONENT FROM SAMPLED DATA. That is why you need a hardware filter before the DAQ device.
What are the specifications of the signal conditioner (hardware module)? Does it have any filtering?
I note that the datasheet for the load cell mentions that the screen (shield) lead of the cable is not connected to the body of the load cell. You may need to add a connection to the mechanical parts to help reduce the 50 Hz component.
Lynn
05-01-2016 07:44 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks Lynn. I have attached the Excel file with the raw data.
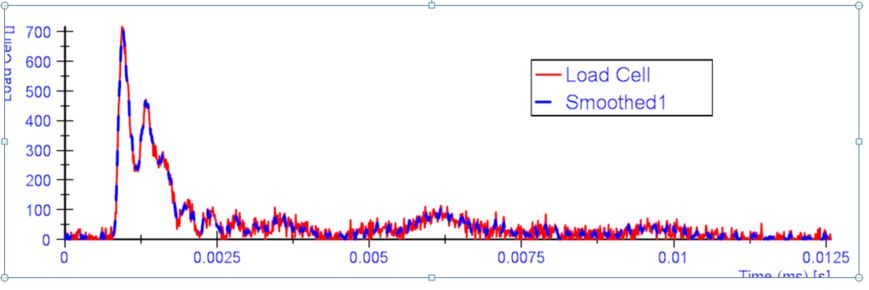
The load was measured with the load cell. An accelerometer was also used for comparison. I have used a low pass filter on the acceleration signal to remove the noise. The oscillatory parts look to have the same trend, but with a difference in the peak amplitudes. I guess this is because the accelerometer has higher resonance frequency and that the load cells have lower loading – unloading rate (strain gauge based load cell).
The hardware module is the pxi 4331: http://www.ni.com/datasheet/pdf/en/ds-268. It contains anti-alias filters. The load cell is connected directly to the terminal of the pxi 4331 module as the hardware module provides the excitation. The hardware is then connected with a pxi chassis.
05-03-2016 02:23 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Please let me know whether additional information is needed.
Brad