- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Nyquist theorem - Determination of Sampling Rate - FFT
04-27-2016 11:28 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi guys,
Nyquist theorem – greater than two times the highest frequency component in the signal.
My tests last for 50 milliseconds sampled at 100 kHz.
How can I determine the optimum sampling rate that I can use for my tests in order to not lose the peaks? I am thinking to perform the test with different sampling frequencies and check whether the amplitude vs time is affected. When I plot the FFT, it shows approximately 2 kHz stable frequency (it becomes zero in the x axis).
Shall I perform the same test with the the sampling rate as the only variable and check the amplitude?
04-27-2016 11:23 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi guys,
Nyquist theorem – greater than two times the highest frequency component in the signal.
My test last for 50 milliseconds sampled at 100 kHz.
Based on your experience, how can I determine the optimum sampling rate that I can use for my tests in order to not lose the peaks? I am thinking to perform the test with different sampling frequencies and check whether the amplitude vs time is affected. When I plot the FFT, it shows approximately 2 kHz stable frequency (it becomes zero in the x axis).
Shall I perform the same test with the the sampling rate as the only variable and check the amplitude?
04-27-2016 11:55 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@BradOconnor31 wrote:Hi guys,
Nyquist theorem – greater than two times the highest frequency component in the signal.
My tests last for 50 milliseconds sampled at 100 kHz.
How can I determine the optimum sampling rate that I can use for my tests in order to not lose the peaks? I am thinking to perform the test with different sampling frequencies and check whether the amplitude vs time is affected. When I plot the FFT, it shows approximately 2 kHz stable frequency (it becomes zero in the x axis).
Shall I perform the same test with the the sampling rate as the only variable and check the amplitude?
The highest frequency you can resolve (Nyquist) is 50 KHz. The lowest frequency will have a period of 50 msec, so 20 Hz. Your spectrum will have points at 20, 40, 60, ... 49980, 50000 Hz (though the last value is really "incomplete", as it has magnitude, but no phase).
Bob Schor
04-27-2016 01:02 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
More strictly speaking, the sampling theorum requires that the samples must be acquired at at least twice the rate of the bandwidth of a bandwidth-limited time signal. As an example, if you've properly filtered a signal which only has components from 0.9 MHz to 1.0 MHz, you don't need a 2 MHz sample rate - you only need a 200 kHz sample rate. The resultant FFT, of course, has no information about components below 0.9 MHz.
It's a common misconception that the rate has to be twice the highest frequency of interest.
Best regards,
Dave
Sr. Test Engineer
Abbott Labs
(lapsed) Certified LabVIEW Developer
04-27-2016 01:19 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
This is not something which is usually determined by experiment. Certainly your approach of sampling at what you believe to be a high enough rate and then looking at the spectrum of the result can provide some clues. However, it can be quite difficult to prove that you do not have any aliased components in the results.
What do you know - from theory, or other non-measured sources - about the bandwidth of the signal, any interfering signals, and the noise in the system? Those are the things which determine the required sampling rate.
"My test last for 50 milliseconds sampled at 100 kHz." This sets a limit on the lowest frequency you can detect and a limit on the frequency resolution you will get from the FFT. It does not tell anything about what frequencies are present in the signal.
"...approximately 2 kHz stable frequency (it becomes zero in the x axis)." What do you mean by the part about zero in the x axis?
Other considerations include the waveform of the signal being measured and what you will do with the data after being acquired. If you have a 2 kHz signal with a complicated waveform (or even a very simple one with a low duty cycle), 100 kHz sampling might not be fast enough to collect all the information about the signal.
Lynn
04-27-2016 01:35 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Duplicate post. Let's keep the discussion in the LV thread where you will likely get more responses.
Lynn
04-27-2016 01:37 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Duplicate post. Let's keep the discussion here. I posted a comment similar to Bob's in the other thread along with a request for more information.
Lynn
04-28-2016 10:51 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks guys,
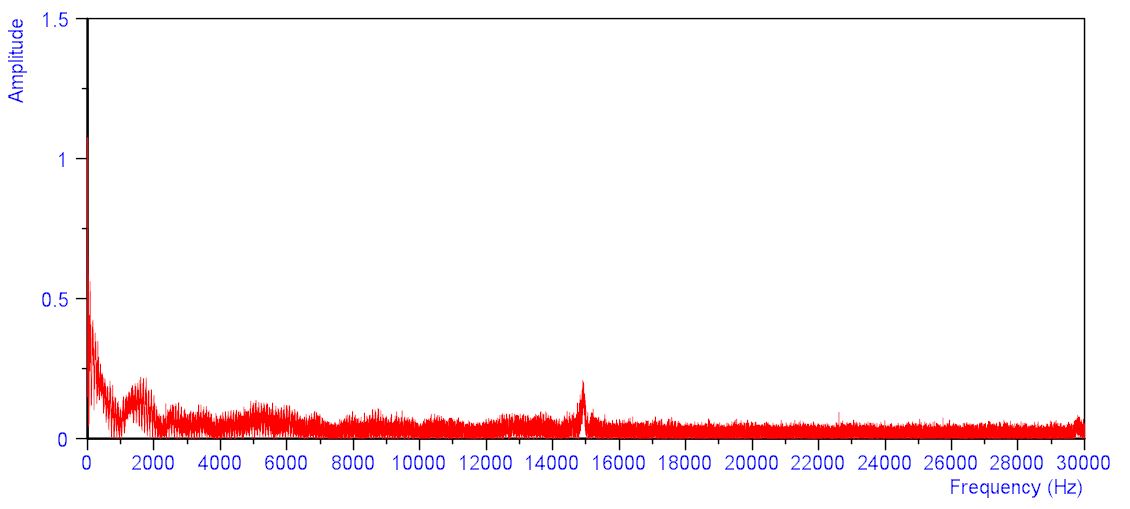
Graph shows that frequency drops to zero at 2 kHz and therefore what I understand is that the bandwidth of the filter should be between 2 kHz – 50 kHz (Nyquist). 2 kHz x 2 = 4 kHz sampling.
04-28-2016 01:54 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
What? Are we looking at the same graph? What's that spike at 15KHz? What about all those lumps and bumps below 10KHz? If you make the filter go between 2KHz and 50KHz, you'll eliminate the majority of your signal. If your Nyquist frequency is 50KHz, then you need to sample at "twice the Nyquist frequency" which is not 4KHz.
Or did I not understand your last post?
Bob Schor
04-29-2016 05:09 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
There are oscillations below 10 kHz and a peak at 15 kHz, but the frequency seems to stabilise after 15 kHz, despite the fact that there is too much noise in the FFT.
The intention is to use a low pass filter (Butterworth) to filter the high frequencies of the signal and also to correct the phase in the initial aplitude-time graph.
If I use sampling frequency 100 kHz , then the Nyquist is 50 kHz, I agree with that. But I want to use different sampling rates to establish which sampling shall I use, this is where I am confused. Also, what shall I use to filter the signal without eliminating the peaks or the majority of the signal?