- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to find local extrema in matrices / 2D-arrays
08-11-2016 09:39 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I am looking for a solution to find local maxima in 2D arrays. Something like the PeakDetector.vi does but for 2D data.
08-11-2016 11:12 AM - edited 08-11-2016 11:13 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
For absolute extrema, you can use Array Min & Max. It is polymorphic to accept multiple dimension arrays and will give you the value and location of the extremum.
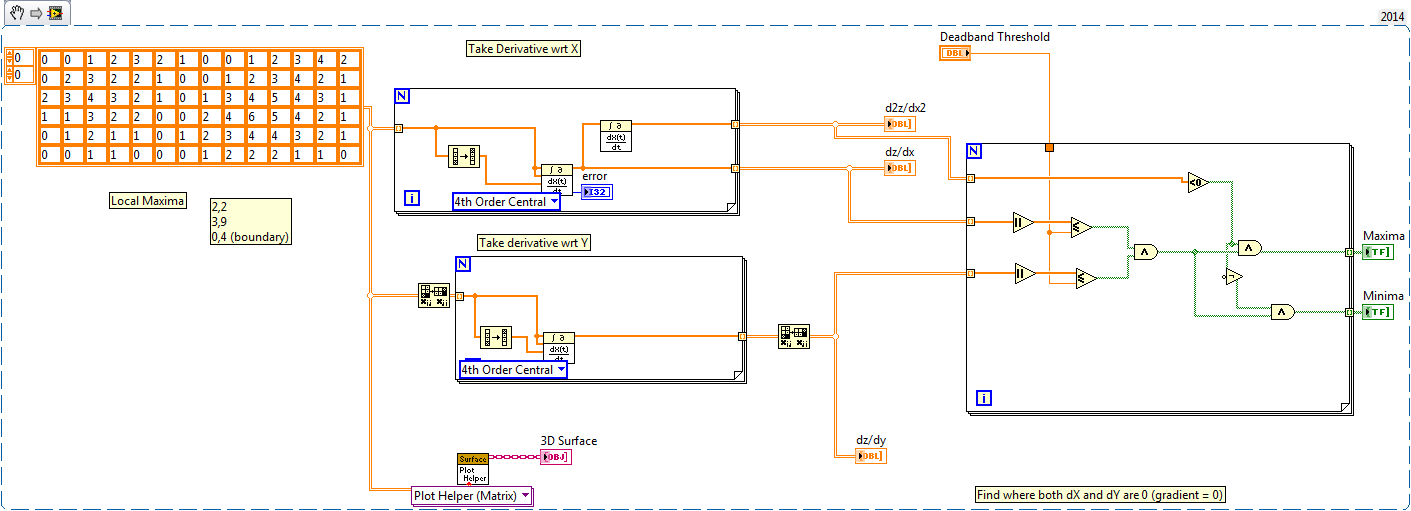
Local extrema are a bit harder. I don't know of any out of the box tool to do that for you, but basically all you need to do mathematically is find the gradient and the location where it is equal to 0 (or close enough to 0). The gradient is just [dz/dx, dz/dy].
You can use transpose array and then apply the derivative VI for each row. Then look for where both are 0 (or within a deadband). To determine whether they are maxima or minima, take the second derivative in one direction (there is no real need to do it in both directions, because if it is truly a local extremum, then both second derivatives will have the same sign.
I coded this up, quick and dirty. Hopefully it is a starting place for you.
08-11-2016 11:49 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
How many local maxima do you expect and are they always in approximately the same location. Do you only need the quantized location or can the peak indices be fractional? Do all peaks have similar width?
Do you have some typical data?
08-12-2016 01:43 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Christian,
I put some sample data to a constant in the VI attached.
08-12-2016 02:56 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
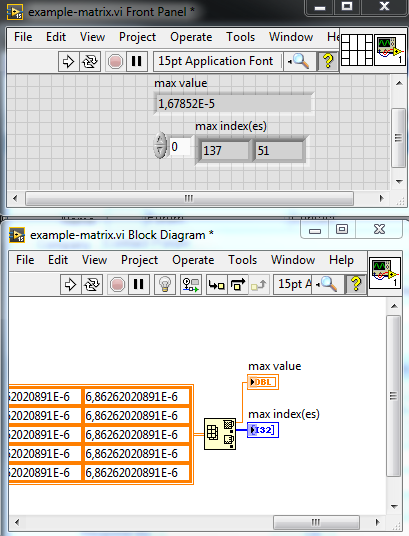
What about that?
08-12-2016 04:56 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
That will just give me one maximum and not the other local maxima...
08-13-2016 02:27 PM - edited 08-13-2016 02:28 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@Standardnutzer wrote:I put some sample data to a constant in the VI attached.
Well, so which local peaks do you want? I can see about three, see image.
As I asked before, are all data sets similar (e.g. similar width of the peaks, similar locations, similar shape and symmetry, etc.) or is each dataset very different?
The data looks like some low order spherical harmonics projected on a plane. Is this theoretical noiseless data or a real measurement (I cannot easily tell if there is noise).
If it is simulated data, what is the math behind it? maybe you can fit to the actual model function and get the entire shape.

08-16-2016 07:16 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Christian,
There is no function to describe the data.
In the mean time I just took the easy approch and looked for the maximum values with certain minimum distances to each other.
I think this will do the job for the moment.
Thanks!
08-16-2016 08:09 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
08-16-2016 09:18 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Ben,
Thanks for your VI. I will give it a try.