- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Create sine wave that smoothly changes amplitude and frequency
Solved!05-11-2019 11:05 AM - edited 05-11-2019 11:10 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
I'm using a sine and cosine function in order to make a circular motion for two servos.
At the moment I'm using a regular sine function (see attached code) in combination with a tick count in order to make the single value fall and rise in a sine function. However, as I increase the frequency or amplitude the sine value changes instantly which makes my servo motors move very quickly obviously.
I would like to make this change slowly but I'm pretty lost how to code this.
I suppose I should in some way have values added to my current value (or latest value) instead of calculating the value it directly.
Can anyone help me with this problem?
Furthermore I'm more than open for ideas on how to smoothen out the signal to the servos in general in order to make the motion more smooth and not as steps. I guess the only solution is a faster loop-time?
Thanks
Solved! Go to Solution.
05-11-2019 12:43 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Haven't looked at your VI in depth, but the way you are calculating Sin and Cos seems strange to me.
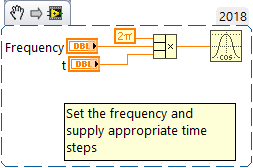
There are a couple of ways you can set up the calculation, both sin and cos expect the input in radians, to convert to a specific frequency then you want to have 2*pi*f*t as your input. See below. This will give a sin/cos at a specific frequency.
The other way is to assume your output has a fixed sampling rate, Fout, then you could do something like the following
In the last method, you are supplying integer steps. To convert to time then divide step by Fout.
mcduff
05-11-2019 01:59 PM - edited 05-11-2019 02:05 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
05-11-2019 02:02 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Are you sure you use of "tick count" is proper? Did you ever probe the values going to the trig functions?
05-11-2019 02:47 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Looks very good and I can customize it to my needs. However I would also like to change the amplitude in the same way which is currently done by multiplying the amplitude and adding the middle value for the dutycycle which I want as output. However this will still make the dutycycle "jump" from one value to another.
Nevertheless many thanks for your help.
05-11-2019 03:24 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
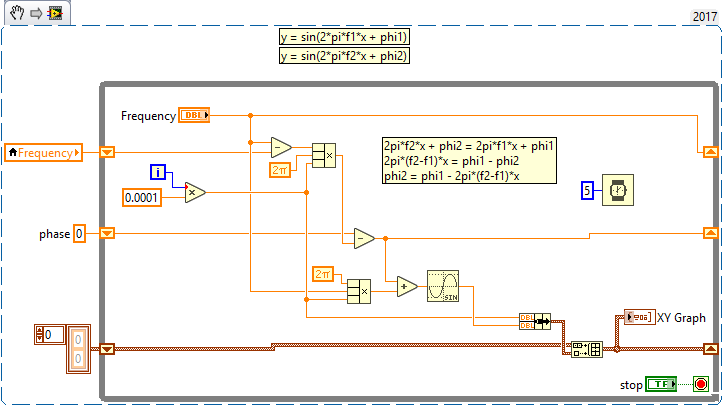
Suppose you know the angular velocity of your wheel (I'm going to call it "omega") at time t, know the current position of the wheel (I'm going to call it "theta"), and the sampling interval dt, and want to know the following three things: the new position of the wheel (this is easy -- it is new-theta = theta + omega*dt), and the sine and cosine of this new angle. This is most easily done using Complex Arithmetic and changing coordinate systems between Polar and Cartesian. Oh, yes, omega and theta are in radians/sec and radians (so I don't have to mess with twopi).
Let's create a plot where Velocity starts at 0 rpm and increases by 1 rpm/sec and see what happens to the the position theta, sin(theta), and cos(theta) as we step in 0.1s steps from 0 to 30 seconds.
First, I want a function that takes theta (initially 0), omega (initially 0), and dt (0.1) and returns me an updated theta and its sine and cosine. Then it is only a matter of keeping track of these values and waiting for 30 sec/dt = 300 time points. Here's the Update function:
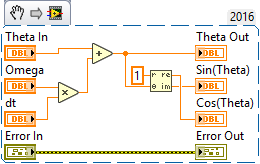
Note the use of Polar to Cartesian (in the Complex Numeric sub-Palette) to get me sines and cosines. So now we just generate our positions (handling the conversion of 1 rpm into radians/second, which we only have to do once). Actually, I'm going to show you only the Front Panel of the VI I made using Update Wheel. This should be an easy exercise for you, and will demonstrate (as shown in the Front Panel) that you can easily generate a smoothly-changing Frequency sinusoid (it's "smooth" because I change frequently "smoothly" and slowly, only 1 rpm/sec = 0.1 rpm/tick). You'd want to also "smoothly" change amplitude, again by every delta-t, changing it a little bit until you reach the value you want.

The Update Function above is a Snippet, but I'm also attaching it as a LabVIEW 2016 VI.
Bob Schor
.
05-11-2019 08:47 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I assume you figured out how I made a "smoothly-changing frequency", namely by changing the rotation velocity of the Wheel with a ramp (or any other function without large "steps" -- it could have also been a sigmoid curve, for example). So if you also want to change amplitude without introducing discontinuities, all you need to do is to multiply the Wheel position (which controls the timing of the waveform) by a similarly-smoothly-changing amplitude function. If I still have the code I wrote for this example, it shouldn't take me more than 10 minutes to add "Amplitude" ...
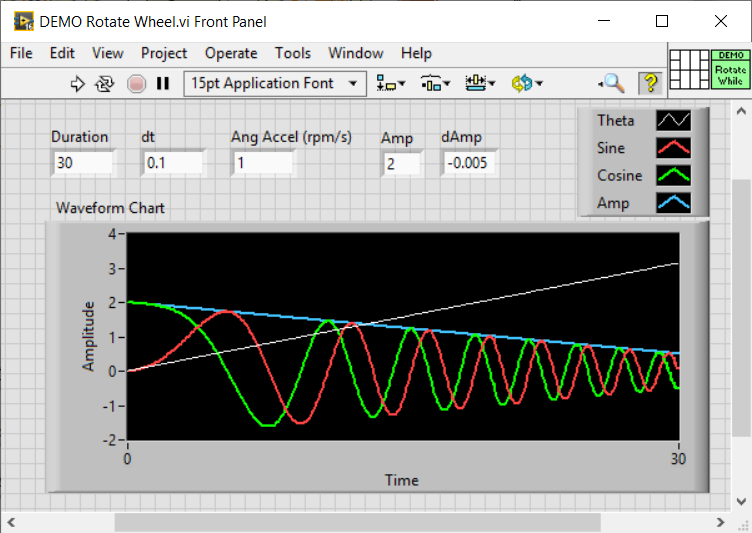
It took 12 minutes. I added an Amp input to the Update routine (it replaces the "constant amplitude" of 1 in that function) and just needed to incorporate the ramp change. Something that should be obvious (I hope) is that the frequencies of the sinusoid "carrier frequency" needs to be significantly higher than the frequency (or reciprocal time interval) over which you make the changes to Carrier Frequency (FM) or Amplitude (AM). Congratulations, you are simulating AM/FM transmission ...
Bob Schor
05-15-2019 09:05 AM - edited 05-15-2019 09:07 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@Bob_Schor wrote:
Add Variable Amp
I really appreciate Bob's beautiful .vi -
just wanted to add:
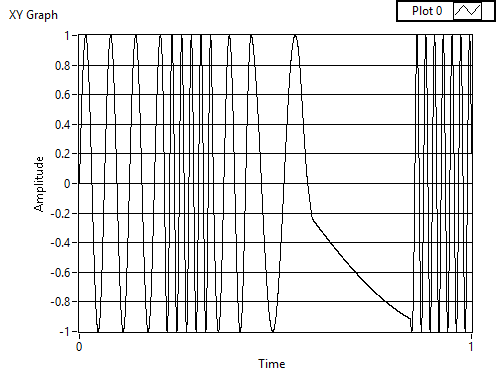
The graph above reminds me of https://zone.ni.com/reference/en-XX/help/371361R-01/gmath/fresnel_integrals/
09-15-2021 01:48 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
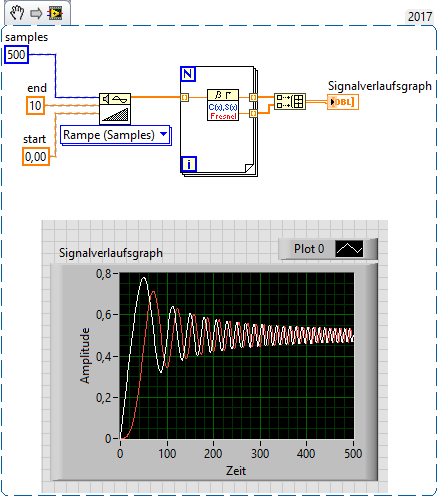
Hello,
could you convert VI into 2017 Labview version? I would be grateful for help.
09-15-2021 01:54 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator