- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Crating a waveform with a clocked loop
Solved!12-06-2019 06:55 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello,
In the vi embedded, if you put the variable "vitesse" equal to 10 (for example), the output called "angle_apres_vitesse" goes from 0 to 719,9 periodically like a saw tooth. Each 10 ms the variable "angle_apres_vitesse" is updated inside a clock loop. I would like to create a waveform that depends of the variable "angle_apres_vitesse" and the elapsed time. But the problem is that this value is not inserted into a table every 10 ms, this is just a simple value that is updated every 10 ms.
My idea was to create a virtual channel in order to generate this waveform, I see I have in my NI instruments an interface called "dev1". If I create a virtual channel with a physical name Dev1, it doen't work and if there is no physical name filled, it doesn't work either.
Anyone would have any idea to create a virtual channel in that case, or maybe there is another solution I haven't think about yet. Any suggestion.
Thanks for your help.
Best regards,
Fabien
Solved! Go to Solution.
12-06-2019 07:28 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
12-06-2019 07:35 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Do you know about LabVIEW's "Waveform" construct? This is a Cluster meant to represent Sampled Data, consisting of three parts: t0, a TimeStamp when the first point is acquired/generated, dt, a Dbl representing the time between samples (1/sampling rate in Hz), and Y, an array of Dbl representing the data. Thus a cluster with an array of 1000 Y values and dt = 0.001 represents 1 second of a waveform sampled at 1 kHz.
Now examine the Waveform Palette on the Block Diagram. Notice that it has sub-Palettes for Analog Waveforms, including a sub-Palette for Generation, including Simulating a device (where you have the choice to generate the points "as fast as you can" or, indeed, at the Sample Rate you specify).
This, it seems to me, is precisely what you are trying to do. If you want to learn how to "do this yourself", let us know and we can critique your code. If, however, you just want to use a generated Waveform (to do something more interesting), let LabVIEW do the Waveform Generation for you and use the Waveform data it provides.
Note that there are functions on the Waveform Palette that will take your Waveform (a Cluster) and return just the data (the Y component -- of course, if you understand Clusters, you can do the Unbundling yourself). So you could use a Simulate a Sinusoid, tell it you want 1000 points at 1 kHz, and once a second, you'd get an array of 1000 points ...
Bob Schor
12-07-2019 02:41 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello,
Thanks for your replies.
@ Bob_Schor
Yes I know a little bit about wavefor construct and you are right I need to generate the points at a sample rate I specify. In my example, I have chosen 10 ms. But this is not the only thing I need to do. That's why I try to construct waveform by my own. But tell me if you think this is not a good idea. If I can simplify much better it will be. But first let me explain what I want to do.
I need 2 more things :
- I need to be able to change the frequency of the saw tooth whenever I want with a parameter ( a number in the front panel). The vi I have embedded can do that with a number updated every 10 ms, the parameter is "vitesse" in my vi. Can the waveform construct do that ?
- The final waveform I want to generate is not really a saw tooth. In fact I use a saw tooth as an input to generate a number scaled every 10 ms based on the saw tooth. This number generated every 10 ms will be my output waveform and this waveform has nothing to see with a saw tooth in fact.
I see on this page https://zone.ni.com/reference/en-XX/help/371361R-01/lvwave/waveform_scale_and_offset/
it is possible to scale the waveform with this parameter :
"scale is the number by which you multiply the waveform data values. A value of greater than zero but less than 1 decreases the waveform amplitude. A value of greater than 1 increases the waveform amplitude. The default is 1.0. "
But my scaling has nothing to do with a simple coefficient. I use a table that gives me for each number between 0 to 720 a number that cannot be generated by a simple calculation. The number has to read in the table.
So do you believe I can achieve that with a waveform construct or do you have any other suggestion to help me solve that problem ?
Thanks for your help,
Regards,
Fabien
12-07-2019 04:25 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
When you generate a waveform using a digital computer, you generate "points" (or "samples") at discrete time points. Let's consider a 1 Hz sinusoidal waveform, and let's consider that we want to approximate the (continuous) sine wave by points every 10 msec. Let ts be the sampling time (e.g. 10 msec), and let fs be the sampling frequency (fs = 1/ts, so for ts = 10 msec, fs = 100 Hz).
Here's an equation for the i-th point of a digitally-generated sinusoid with sampling time ts, Amplitude A, frequency f, and phase p: wave(i, (ts, A, f, p) = A sin (i * 2*pi*f*ts + p).
It is easy to make a 1 Hz sinusoid sampled at 10 msec intervalues with an Amplitude of 1 phase of 0 -- generate 100 points wave(i) = sin (i * 2*pi*0.01), i = 0 .. 99, and "play" this waveform continuously at 100 Hz. As long as you keep generating these 100 points over and over, your waveform will continue.
But what if you want to change it? Ah, now it gets interesting. When do you want to change it? "Right now", or "at the end of the last full sinusoid"? What do you want to change -- A, f, p?
One way to change the frequency of the sinusoid is to change the sampling frequency, fs (or, equivalently, ts). Suppose you played the same waveform of 100 points at 1 kHz -- you'd get a 10 Hz waveform that lasts 0.1 , (but you'd do it over and over, so it would just be a 10 Hz wave). What if you wanted it 100 times slower? No problem, play the points back at 1 second intervals ... oops, now we have a "steppy" sinusoid, where the value is constant for a second, jumps, is constant for another second, ... Probably don't want that. How do you fix it? Change fs from 1 to 100, and generate not 100 points, but 100*100 points for the waveform.
So you need to think carefully how you want your digital waveform generator to work. When things don't vary with time, it's easy -- generate a periodic waveform and play it over and over. When you need to change, you will need to think about how you make transitions in changing your parameters (I haven't even begun to talk about whether the parameters change as a function of time, or whether they "jump" from one value to another).
If you start to think about it, you'll realize that there are "interesting" relationships between how smooth you want your transitions to be, how much of a waveform you can "pre-compute" (and therefore "play" nicely), the speed of the basic sampling loop (I'm assuming you'll keep its frequency fixed, and recommend that you pick a nice round number, such as 1 kHz or 1000 points/sec, for now). Incidentally, how do you pick a good sampling frequency? Depends on your signal, but you'll want to be a factor of 10-100 greater than the maximum frequency of your signal to avoid the "stair-step approximation" we saw a few paragraphs ago.
OK, end of lecture. I think (and hope) the answer to your questions are in there, somewhere ...
Bob Schor
12-07-2019 06:46 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Well, your example of the digitally-generated sinusoid is good to explain the 2 ways to change the frequency (changing the sampling time ts or the frequency directly).
And you explain very well the problem concerning the steppy frequency (when the frequency is low), it is a good reminder for me but it was not exactly that question I wanted to be answered.
To answer your question with the analogy of my case, I just want to change the frequency, nothing more. The frequency has to be changed as soon as I change the value of my parameter "frequency" when the "vi" is running and it has to be changed "Right now".
Here is how I determine the value of the sampling rate ts:
With the maximum frequency I need to drive the signal I determine the minimum accuracy I want, I mean the minimum time elapsed. I select then the sampling time according to this accuracy and I let it fixed for the rest of the program.
I already have though about that.
My question was how to create a waveform with a value that is updated every 10 ms in a clock loop ?
Maybe this is something too easy for you, but I have no idea about it.
Fabien
12-08-2019 11:37 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
You have several things that you need to manage, but, fortunately for you, LabVIEW is designed to allow you to do this.
- You need to run a loop every 10 msec, updating the current value of "time".
- You need to use the current value of Time and the current value of Frequency (as well as the other fixed parameters of your waveform) to output the current value of the Waveform.
- You need to do all this while allowing the User to change the value of Frequency.
LabVIEW uses the Principle of Data Flow, which allows it to do several independent things (like updating the Waveform and updating the Frequency) at the same time with minimal interference with each other. It also embeds the concept of time as a primitive (most other programming languages emphasize running "as fast as they can").
I'm sure you are familiar with the Timing functions. A particularly useful one here is the "Wait until next ms multiple", as you can use this to build your "clock", a sub-VI that if you call it at least as fast as it "ticks", can return the next "clock time point". You can use this to build a sub-VI called "100 Hz Clock" that gives the "next time" of a clock every 10 ms, and also serves as a "delay" so that the loop it is in runs at 100 Hz.
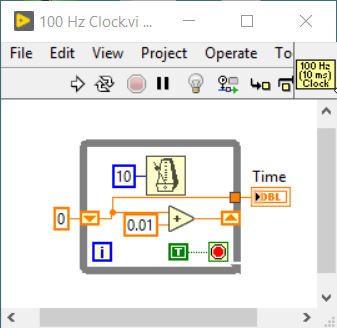
The principle is simple -- you create a "do-once" While Loop (have you learned about these? They consist of a While Loop with "True" wired to the Stop Indicator -- it will run once, then exit). While Loops can have Shift Registers, which function as "local memory". Let's create one and have its output be called "Time", and have it increment by 0.01 (seconds, or 10 msec). Here is most of this function -- it needs one last change to make it work properly (which I'm leaving to you to do -- create it yourself from the picture, then test it and see if you can figure out the final step). I did not create this as a Snippet -- it is so simple that it should take no more than 2 minutes to create in any version of LabVIEW, and will teach you some lessons about Shift Registers. Also note that I created a really simple Icon for this VI, which means if I use it in another Block Diagram, I'll know what it does!
So now you need another While Loop, with the 100 Hz Clock inside it to both "time" the loop (making it run at 100 Hz, or once every 10 ms) and provide you the Time component that you need to multiply by 2pi and by the sinusoid's frequency, add the phase, take the sine (found on the Math Palette), and finally multiply by the amplitude A. This will take far less than 10 msec, so the Principle of Data Flow says that the slowest thing (the "Clock") will determine the loop time.
But you want a variable Frequency! One way (the easiest) is to simply put the Frequency Control inside the While Loop that computes the Sinusoid. It will get read every 10 msec, so you'll always have the "up-to-date" value available, at the (relatively minor) cost of re-reading it all the time. There are ways to skip this repetitive re-reading of an unchanging control (something called the Event Structure), but that's another topic ...
Bob Schor
12-09-2019 05:07 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Yes I am familiar with the timing function.
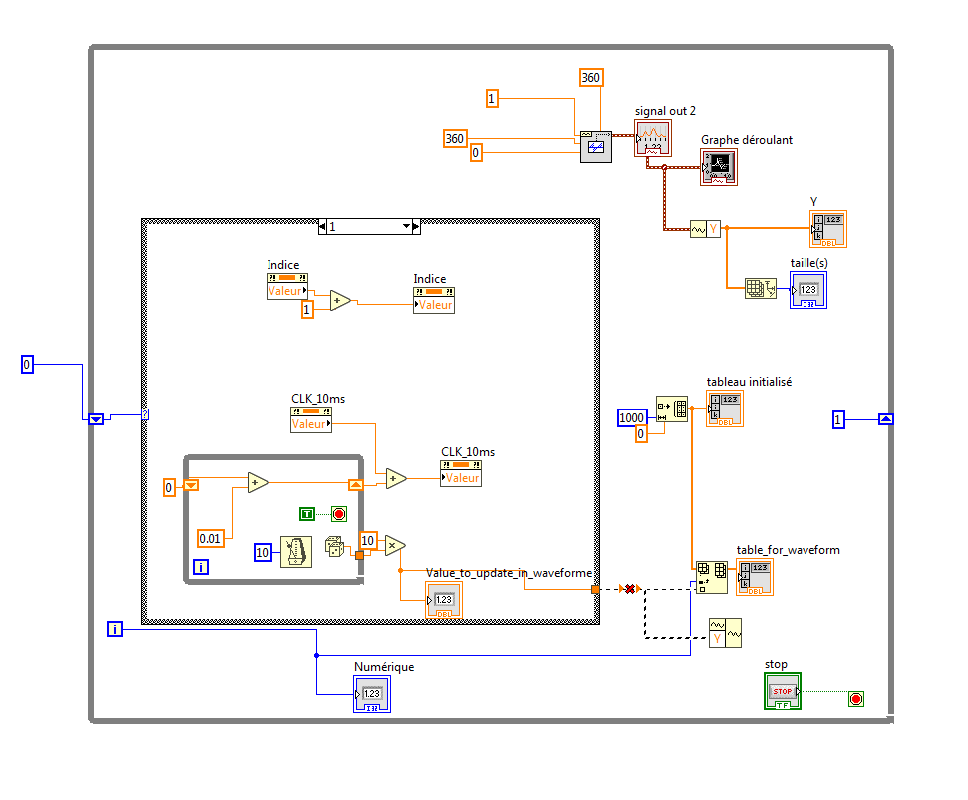
I have done it but I still do not know how to convert a value updated every 10 ms in a waveform.
The input of the waveform generator has to be a 1D table. In my case this is a value, so it is not compatible with a waveform.
In the example below, can you tell me how do I connect the waveform with the value updated every 10 ms called "value_to_update_in_the_waveforme" ?
I also try to copy the variable "value_to_update_in_the_waveforme" in a table but nothing is written in the table. My idea was to use that table to create the waveforme, but if nothing is written inside, how can I do ?
Regards,
Fabien
12-09-2019 05:20 AM - edited 12-09-2019 05:22 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Fabien,
you really should learn the LabVIEW basics, like how to handle arrays in shift registers:
That while loop inside the case is completely Rube-Goldberg.
"Indice" and "CLK_10ms" should be stored in a shift registers, too.
12-09-2019 08:13 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Fabien,
Sorry, I missed a few points.
- Your waveform is a triangle wave, not a sinusoid, so your function needs to be (naturally) a Triangle function. I assume you know that this is just the "Mod" function, where the divisor is the Period of the function, and the function value is the Remainder.
- More important, I forgot another important point -- you are indexing your function with a value that depends on the product of Time and Frequency (and, hence, is dimensionless). As this Index function increases in a "continuous" manner, the function it is indexing also increases continuously. But what happens when you "jump" the frequency? You also "jump" the index, and create a discontinuity in your function. Note that this might be OK, but you probably want to have the function remain continuous at this point and have its slope suddenly change, right?
- The "easy" way to do this is to note that the function argument has three variables -- Time, Frequency, and Phase. The simple way to get continuity is to change Phase at the same time that you change Frequency. The math is fairly simple -- Time stays the same (it's the Time that you start to use the next Frequency). If the old frequency is f0 (and the phase is P0), and the new frequency is f1, with the time of transition being t1, then you want f0*t1 + P0 = f1*t1 + P1 (the argument for your sinusoid or triangle wave at time t1 with the "old" parameters f0 and P0 should be the same as the argument using the new parameter f1 and the to-be-determined parameter P1 so that the waveform is continuous at t1). Solve the above equation for P1 and use it.
Bob Schor