- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- « Previous
-
- 1
- 2
- Next »
Calculate sinusoidal Position from acceleration data
12-02-2019 03:34 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
You have harmonic motion at a frequency f:
Acceleration = A Cos[2 pi f t]
Velocity = A / (2 pi f) Sin[2 pi f t]
Displacement = - A / (2 pi f)^2 Cos[2 pi f t]
You can do this in frequency space, the FFT will give you the amplitudes at a particular frequency, or you can fit your data to Cos, then divide by (2 pi f)^2 for displacement.
mcduff
12-02-2019 03:38 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
12-02-2019 03:49 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@ASTDan wrote:
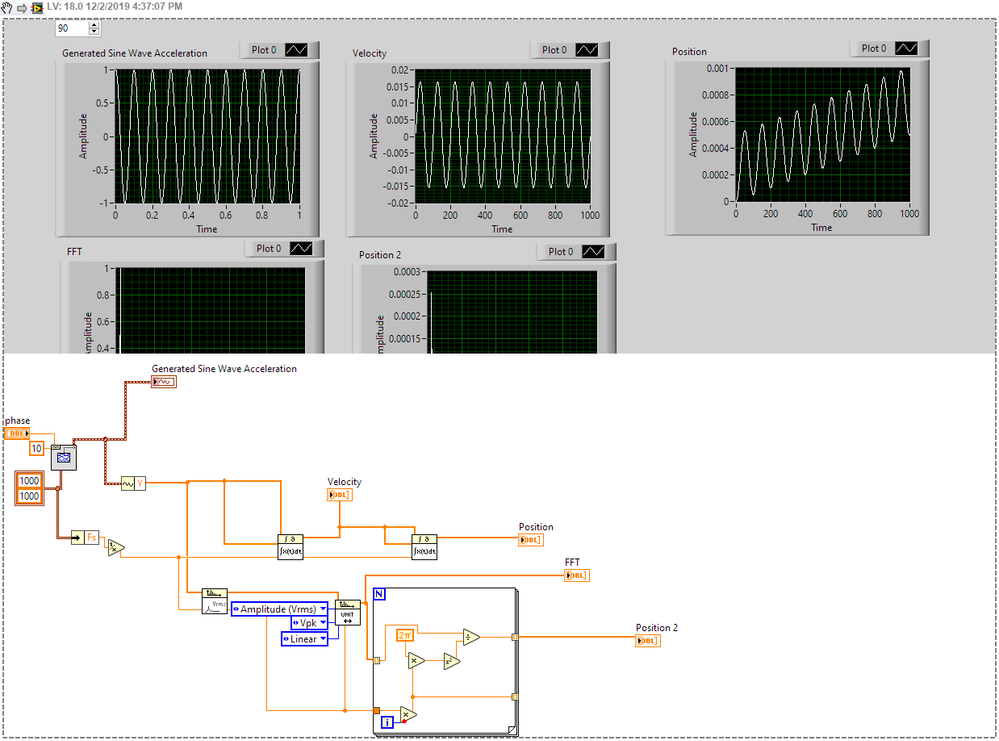
So here is my implementation to calculate in the frequency domain.
How do I get this data back to the time domain?
That is harder, you would need to keep the complex FFT, divide, then invert. I apologize, I thought you were looking just for an amplitude for displacement.
Otherwise high pass, integrate, high pass, integrate.
mcduff
12-02-2019 03:56 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
12-02-2019 04:58 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I keep starting replies but don't get a chance to finish before the thread has moved on without me.
The highpass problem you're seeing is the transient response of the filter. It's not generally avoidable. I don't recall all the math, but I'd venture that the transient for a 1 Hz highpass is pretty well gone after 4 or 5 seconds. Try generating 10 seconds worth of sine wave, but only display the last 5 seconds worth of the Vel and Pos integration results, after the filter transient has faded away.
3 different approaches have been mentioned and each has distinct pros and cons.
In the time domain, you can use highpass filtering but then you'll be stuck with its transient reponse. Or you can subtract off a simple mean value, but that'll also produce artifacts unless your sine wave freq, your sample rate, and the # samples in your chunk of data are all in just the right proportions. Often you'll be stuck with less-than-ideal proportions. (Also in the time domain: subtract out a best fit line *after* integrating. This is substantially similar to subtracting the mean *before*, but not quite exactly the same.)
In the frequency domain, you can determine amplitudes at specific frequencies but again, you'd need some different special proportions among sine wave freq, sample rate, and # samples in the chunk of data. Otherwise you get spectral leakage and error in your amplitude measurement. LabVIEW has a pretty nice tone detection function that can compensate for some of that, but I don't have extensive experience with it personally.
These basic approaches don't completely solve your problem perfectly, so you'll have to refine these techniques with some detailed coding.
For example, if I were to tackle this using an approach that subtracted the mean before integrating, I'd be aiming to do some of the following:
- use a sample rate at least 20x the sine wave freq.
- figure out a way to process an integer # cycles of the sine wave at a time (and preferably a fairly large integer, perhaps 20 again). Most likely this involves finding successive peaks or zero-crossings so you can extract subsets of the accel data that has integer #'s of sine cycles
- discuss with the customer. Maybe some valid simplifying assumptions can be made. Or maybe you've already made too many, and the real situation is even more difficult to deal with. (For example, the previous effort to get integer #'s of sine wave cycles in a chunk of data depends on a well-behaved waveform that has 1 fundamental frequency.)
-Kevin P
12-02-2019 05:38 PM - edited 12-02-2019 05:41 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
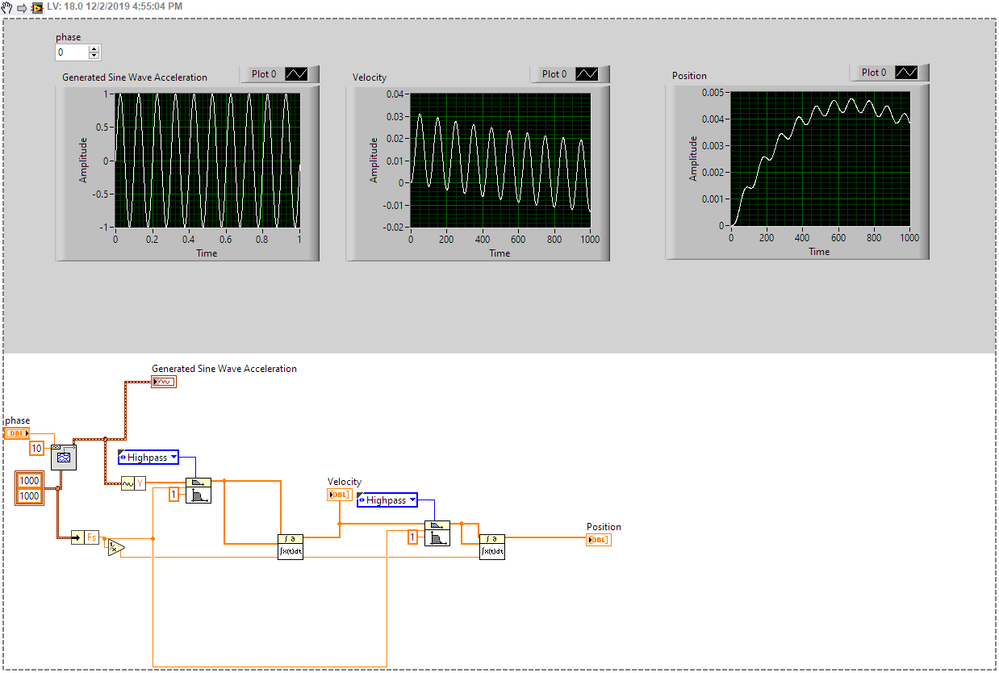
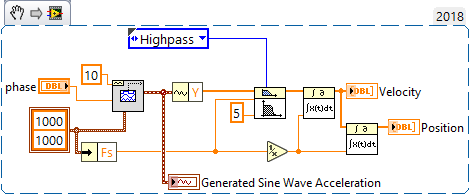
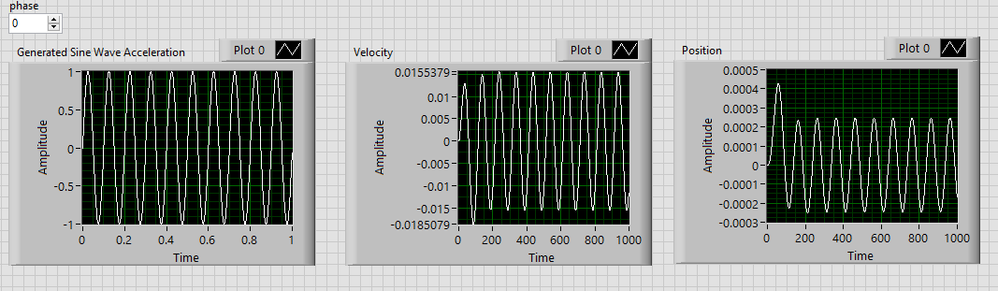
Here's a quick implementation. There is something wrong with your code, see below.
Your signal is clean so I didn't implement a second high pass, which you can do.
Most Important. Your high pass filter is wired incorrectly. Wire the the stop band to the low frequency cut-off. Look at the help.
mcduff
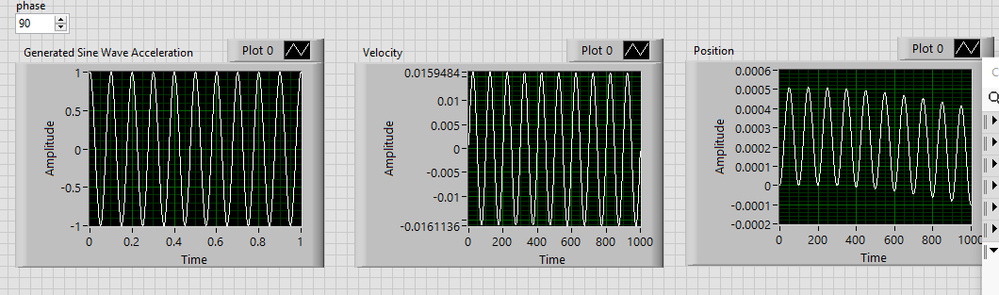
PS You will see that phase does not matter here, I set it to 0.
Edit: Showed the wrong picture for 0 phase, below is zero phase.
12-03-2019 07:53 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Kudos to Kevin and Darin's posts.
Punch above my weight class...
Those tow "c" values in this situation would be the position and velocity at a given point in time.
If you could "zero" or such the signal at a known position and velocity, you would be able work without the filtering. More on that I a bit.
The digital filters do take some time to get initialized so you have to let them run for a bit before the transients work their way out. There are often a "rest" input on those filters that should be used to ensure they are rest to start and then run without the reset.
But now is the time to think about an alternative to using the accelerometer. Keyence makes some impressive distance measuring stuff that would let you measure the position directly instead through the back door. They could be zeroed and can be very accurate and be able to reflect changes if the frequency of the motion changes while the accel. approach could have trouble if the filters end up damping the response.
Nuff for now,
Ben
12-03-2019 08:44 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks the reminder. I missed you need to wire the High Pass cutoff into the Low Pass cutoff frequency when high pass filter is selected. Very intuitive 🙄
Playing around with my data it looks like the more filtering I do the better the signal. However I lose low frequency data. That makes sense.
I am going to try to sell the FFT of the signal. That might be what he actually needs. Will talk to the customer and let you guys know.
Thanks so much for all the help!
- « Previous
-
- 1
- 2
- Next »