- Document History
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report to a Moderator
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report to a Moderator
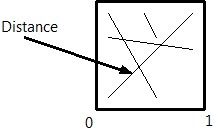
Challenge mathématique #40 : La distance moyenne dans un carré
Pour janvier et afin de reprendre en douceur, un algorithme simple à réaliser (moins par calcul manuel). Quelle est la distance moyenne entre deux points dans un carré de coté 1 sachant que leurs coordonnées suivent des lois du hasard uniformes sur [0,1] ?
En effet, certains points peuvent être positionnés en diagonal (proche des coins opposés) donc les plus distants que 1 et d’autres plus parallèle à l’un des côtés donc inférieurs à 1. La moyenne n’est donc pas triviale.
Le défi est d’écrire un petit code LabVIEW qui évalue cette moyenne en utilisant une vérification de manière brute (Pas le résultat numérique direct d’une formule toute faite).
L’algorithme sera validé par l’obtention de 6 chiffres après la virgule, stables à chaque lancement du code.
Vous pouvez vous servir du code Joint comme point de départ (Version LabVIEW 2010)
Pour le prix il reste encore quelques livres LabVIEW 2eme édition à gagner avant de changer de prix. Le gagnant sera tiré au sort (basé sur les sorties du loto) sur les codes validés.
Envoyez votre code renommé Distance moyenne carré_ Mon_Pseudo_ici.vi à emmanuel.roset@ni.com avant le 31 janvier. Et postez sur la communauté « code envoyé » pour vérifier la boite email en cas de non réception.
Je pense que le premier qui trouve la valeur exacte peut la poster pour que les autres la confirme !
Défi complémentaire, faire en sorte que votre code soit le plus rapide !
Défi (encore plus) complémentaire, faire la même chose avec un disque de rayon 1 !!!! avec la même méthode
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Avec les périodes de fêtes, le défi est en ligne avec un peu d'avance pour bien commencer l'année.
Bonne année 2017 !!!!!
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Bonjour Emmanuel,
merci pour ce nouveau challenge, et comme je suis toujours en congés, j'en profite un peu 🙂
Je ne tombe jamais sur la même valeur de distance moyenne! 😞 Ou quelque chose m'échappe, ou alors cette valeur peut varier dans un interval donné!!??!!
A chaque fois, je tombe sur une valeur moyenne qui tourne autour de 0.521400 (de 0.521324 à 0.521467 si j'élimine les extrèmes).
Désolé, mais les statistiques et moi, ça n'a jamais fait bon ménage 🙂 puis depuis les années, j'ai un peu oublié ![]()
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Oui c'est exact une valeur approchante est bien de 0,5214054331672...
Le but est de créer un algorithme qui évalue cette distance moyenne par l'ajout de valeurs successives pour affiner les chiffres après la virgule jusqu'à atteindre une stabilité. L'astuce est de se rappeler comment mesurer les distances avec des coordonnées X et Y.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
merci Emmanuel,
tout le monde doit se souvenir de ce fameux théorème 😉 même après des années, je m'en souviens encore 🙂
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Isaac ASIMOV
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Mon programme tourne depuis maintenant près d'une demie heure, j'ai pas encore de valeur stable, enfin, parfaitement stable 😉
Il semble toutefois tourner autour de 0.521398 de longueur moyenne, mais ça ne rejoint pas l'évaluation donnée par Emmanuel, ça s'en approche!!!
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Pour plus d'éclairsissement il faut se rappeler du théorème de Pythagore. Par contre il y a un piège, c'est que pour atteindre des valeurs de virgules stables au dessus de 3 chiffres il faut un grand nombre de répétition > 100 exp 6 et la RAM du PC en standard va peut être avoir du mal avec une boucle simple. Il faut bien écrire le code avec les optimisations.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
C'est clair que Pythagore nous aide dans ce challenge, c'est bien à son théorème que je faisais allusion ci-avant! 😉
Malheureusement, je n'arrive pas à stabiliser la valeur de longueur moyenne, même après plusieurs centaines de millions d'itérations (calcul de moyenne). 😞
Heureusement, il reste quelques jours pour y réfléchir 🙂
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Pythagore, c'est trop lent. Les complexes sont plus rapide 😉
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Bon, après 50 milliard de valeurs, je ne stabilise toujours pas à 6 chiffres. Je doit mel faire quelquechose? Je stabilise par contre à 5 chiffres plus facilement.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
J'ai le même problème, j'ai beau laisser tourner, je n'arrive jamais à stabiliser!
C'est d'ailleurs curieux vu le calcul de moyenne qui augmente le nombre d'échantillons, chaque nouvel échantillon devrait voir son impact réduit sur le résultat de calcul de moyenne et finir par ne plus en avoir du tout ... en principe.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Bon, je reconnais sur ce coup là j'ai pas la solution. Cette fois c'est un vrai challenge ! J'ai remarqué cela avant de la proposer, sinon c'était trop simple avec quelques icones.
En effet une moyenne sur de plus grands chiffres normalement converge forcément sur un résultat plus précis.
Je me suis posé ces questions:
- Les bornes des générateurs aléatoires incluent-ils 0 et 1 ?
- Le buit aléatoire n'est vraiment aléatoire (pseudo) mais se répète (cela dépend de la fonction et de la sequence)
- les fonctions mathématiques ont une limite en précision, faut il la gérer ?
En tout cas dans un code de mesure, cela peut être utile d'avoir cette précision
L'enquête continue...
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Code envoyé.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Merci Phil58 pour avoir cherché la solution. Le code n'est toujours pas stable et le défi se termine demain.
S'il reste irrésolu, tout le monde pourra continuer à chercher la solution pour trouver un jour une méthode qui stabilise les valeurs !
En attendant le défi de février est lancé ![]()
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Code envoyé
J'ai laissé des commentaires sur les valeurs à paramétrer pour juger de la stabilité du résultat. C'est pas vraiment une solution au challenge, mais plus un outil pour la trouver.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Maiiiis, je ne trouve pas la page du challenge de février ![]()
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Merci Nico_EMC et Phil58
Pour les derniers challenges ils ont disparu des pages il faut rechercher #40 et #41 pour les retrouver. Je suis en train de voir avec notre service qui gère la communauté pour régler ces problèmes et aussi pour que cela soit plus logique et accessible. En fait normalement ces défis apparaissent depuis la fenêtre de lancement LabVIEW mais depuis la mise a jour du site, tout est en cours d'ajustement. Désolé pour le désordre.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
J'ai eu beau chercher, je n'ai pas trouvé, même en cherchant "#41" ![]()
Si quelqu'un avait un lien direct, ce serait sympa ![]()
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Isaac ASIMOV
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Merci Michael ![]()
Et moi, je dois me re connecter à chaque fois que je veux poster un message ... mais c'est peut-être normal!!??!!
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report to a Moderator
Merci pour le lien direct. En effet tout le monde doit se reconnecter à chaque fois pour le moment mais nous travaillons a résoudre tous les soucis pour avoir une bonne expérience avec la nouvelle communauté.