Numeric control value of double type deviates from entered value

[vansoest]

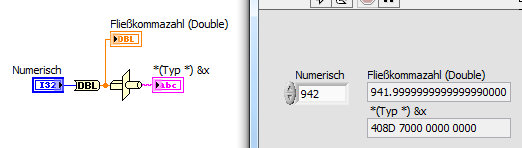
After entering 0.002 in to a numeric control of the double type, the indicator of the same type with 20 digits of precision shows a value of 0,00200000000000000004. And the result of 2 / 1000 is also 0,00200000000000000004. It is not possible to calculate or compare anything with this type of hidden deviations. I also found another comment where a conversion of an INT to DOUBLE had the same result, a deviation of the mathimatical correct valeu. INT 942 converterd to a DOUBLE becomes 941,999999999999999. Is this a bug in labview?

[crossrulz]

---

@vansoest wrote:

Is this a bug in labview?

---

No.  It is a limitation of Floating Point numbers in general.  Every computer language has this issue.  Do a search for equality of floating point and you will find all kinds of threads.  In summary, do not do an Equals comparison with floating point numbers.  You need to check a range or subtract the two values and check to see if they are "close enough".

[GerdW]

Hi,

the only buggy part is the display of the 942 converted from I32 to DBL!

But it's just a bug in the display of that value, it's no bug in the underlying data:

The typecasted string contains too many zeros to hold any fractional part in this DBL value!

[gnorin]

As previously states this is a limitation of floating point. Think of the 2 base that a computer actually uses. Remembering the algorithms for switching between 10 base and 2 base this is what 0.002 would be like:

0.002*2=0.004

*2=0.008

*2=0.016

*2=0.032

*2=0.064

*2=0.128

*2=0.256

*2=0.512

*2=1.014 (our first 1)

0.014*2=0.028

0.056

0.112

0.224

0.448

0.896

1.792

2*0.792=1.584

2*0.584=1.168

And so on….

This is then

0,0000000010000001100010010011… 

which would require way more that 64 bits, or the 52 bits that could actually be used for this in a double representation:

(sign bit, 1)*(value bits, 52)*2^(exponent bits, 11)

So as a result the value is rounded of the the nearest value it can represent which in the decimal, 10 base is not exactly 0.002. 

With 52 bits in the "Mantissa" part of a double floating point the resolution in decimal would be 52*log(2) which is approx 16 digits depending on how you round it (LV says approx 15 digit precision for floating point). The display format of your controller it is probably set to floating point but as stated above this is only a rounding error for the Display of the value and not the value itself. 

Anyway I guess the bottom line is that LabVIEW can display values on 10 base with approx 15 digit precision. 

For comparision of numbers see the link below:

http://www.ni.com/white-paper/7612/en/

Best regards

Gustav

[natasftw]

I typically wouldn't explain this in this setting as it's likely to be more confusing than helpful.  But, with the more confusing (and partially inaccurate) response above.  It's important to bring in some correct information about the actual representation of floating point.

With double precision, we are correctly discussing a 64-bit representation that is split into three sections:

Sign - 1 bit

Exponent - 11 bits

Mantissa - 52 bits

The bits are in that order.  Sign/Exponent/Mantissa.

The sign is easy.  It's a single bit as the value is either positive or negative. 0 is positive.  1 is negative.

Exponent is a bit interesting.  11 bits can represent the values 0-2047.  If we just used that value as 2^n, we'd be able to get some incredibly large numbers.  But, we wouldn't be able to get any fractional values.  As a result, we take the halfway point and use subtraction.  The exponent is calculated as 2^(n-1023).  If we think about that, 2047-1023=1024.  So, we can make some pretty big numbers still.  At 0, we get -1023 so we can make some pretty small fractions with this.

The mantissa is a little bit tricky.  It's the fractional component of a binary number.  That can sound a bit strange.  How does a binary number have a fraction?  Let's look at the binary value 0100.  Typically, we'd see this having a value of 4.  We're assuming there's a decimal point at the far right.  If we move that decimal point such that we'd see it as 01.00, we could see the same 4 bits meaning 1.  If we move it to 0.100, we'd have a value of 1/2.  In floating point, we see it as 1.mantissa  We use that 1 to gain an extra bit of resolution.  The bits in the mantissa make up the entire fraction.  We can use that to create most numbers within a small amount of error due to not having ALL possible values.

Once we have those three components, we create our number by doing simple calculation:

(sign bit) 1.mantissa * 2^(exponent - 1023)

When we see how much goes into this, we notice there is bound to be some quantization error (error created by that resolution not being perfect).  The problem you're running into deals with this.  Things you know are mathematically equivalent won't have that error show up equally.

5/3 ~= 1.66666667

1/3 ~= 0.33333333

5 * 1/3 ~= 1.666666667

But, the quantization error for 5/3 and 1/3 isn't identical. As a result, 5/3 won't be "equal" when compared to 5 * 1/3.  This is where you're going to find a wealth of resources that explain direct comparison of floating point values is dangerous.  While those calculations are known to be mathematically equivalent, it's expected a direct comparison will return a not equal response.  You can follow the white paper linked to get a few ideas on how to work within this limitation.  But, the most important part is knowing the limitation does exist when working with floating point.  It's not a "bug" in any particular language.  All programming languages are affected by this limitation.  It's just a byproduct of how we represent the value in the bits provided.  It has some pros and cons.  This is just one of the cons.

[gnorin]

Oh Im sorry. Just for myself then what is confusing and more important what is inaccurate? 

[Alexander_Sobolev]

Inaccurate is representation of numbers using floating point format.

When number of digits to show is above precision (~15 for double), display can pick any value that is represented with received sequence of bits. He picks 941.9999... . This number for him does not differ from 942.

Do not use displays with precision of more digits that your number has. 

Do not use equal (not equal) for doubles.

[natasftw]

---

 for this in a double representation:

(sign bit, 1)*(value bits, 52)*2^(exponent bits, 11)

---

The first bit with the group of numbers takes some time to understand what you're getting at even with understanding how floating point is broken apart.  It's much easier to understand binary in the way all other binary is approached: a number is the sum of all the 1s in the binary.  1/2 + 1/4 + etc.  When each point is division by 2, it's even more confusing to look at a multiplied solution.

The quoted part is inaccurate.  The representation would be (-1^sign_bit)*(1.52_mantissa_bits)^2(11_exponent_bits-1023).  Understanding why the -1 to the power of sign_bit, why mantissa takes place after the decimal, and understanding where the 1023 come from are integral to understanding the representation.  They're a bit over the head of most people confused as to why things don't equal exactly.  But, when discussed, we should make a point to be accurate about the representation such that we don't cause confusion later on for those that started confused.